题目内容
2．
如图，⊙O的半径为1，AB是⊙O的一条弦，AB=$\sqrt{3}$，则弦AB所对的圆周角的度数为（ ）| A． | 30° | B． | 60° | C． | 60°或120° | D． | 30°或150° |
分析 作OH⊥AB于H，根据垂径定理得到AH=$\frac{\sqrt{3}}{2}$，根据正弦的概念得到∠AOH=60°，根据圆周角定理和圆内接四边形的性质得到答案．
解答 
解：作OH⊥AB于H，
∴AH=$\frac{1}{2}$AB=$\frac{\sqrt{3}}{2}$，
∴sin∠AOH=$\frac{AD}{OA}$=$\frac{\sqrt{3}}{2}$，
∴∠AOH=60°，
则∠AOB=120°，
弦AB所对的圆周角∠ACB的度数为60°，∠ADB的度数为120°，
故选：C．
点评 本题考查的是圆周角定理和垂径定理，掌握同弧所对的圆周角是圆心角的一半是解题的关键，注意锐角三角函数的应用．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
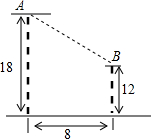如图，要在两幢楼房的房顶A、B间拉一根光缆线（按线段计算），则至少10米．
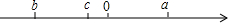已知有理数a、b、c在数轴上对应的点如图所示，且表示数a的点、数b的点与原点的距离相等．
10．下列计算中正确的是（ ）
| A． | $\sqrt{3}$+$\sqrt{7}$=$\sqrt{10}$ | B． | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | C． | 2+$\sqrt{2}$=2$\sqrt{2}$ | D． | $\sqrt{4}$+$\sqrt{4}$=4 |