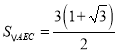题目内容
【题目】如图所示,四边形![]() 内接于⊙
内接于⊙![]() ,
,![]() 是⊙
是⊙![]() 的直径,过点
的直径,过点![]() 的切线与
的切线与![]() 的延长线相交于点
的延长线相交于点![]() .且
.且![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当
,当![]() 时,求⊙
时,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,求阴影部分的面积.
【答案】(1)见解析;(2)半径![]() ;(3)
;(3)![]()
![]()
【解析】
(1)作DF⊥BC于F,根据切线的性质得到∠PAC=90°,根据圆周角定理得到∠ADC=90°,得到∠DBC=∠DCB,得到DB=DC;
(2)根据垂径定理求出FC,证明△DEC≌△CFD,根据全等三角形的性质得到DE=FC=![]() ,根据tan∠DAE=
,根据tan∠DAE=![]() =
=![]() ,求得∠DAE=60°,从而可证得△AOD是等边三角形,则⊙O的半径OD=AD=2.
,求得∠DAE=60°,从而可证得△AOD是等边三角形,则⊙O的半径OD=AD=2.
(3)根据△AOD是等边三角形得∠AOD=60°,再根据阴影部分的面积=扇形AOD的面积﹣△AOD的面积计算即可.
(1)证明:![]() 是⊙
是⊙![]() 的切线,
的切线,
![]() ,即
,即![]() ,
,
![]() 是⊙
是⊙![]() 的直径,
的直径,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
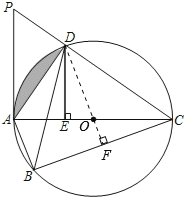
(2)解:如图,作![]() 于
于![]() ,连接
,连接![]()
![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]() 经过点
经过点![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
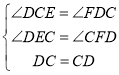
![]()
![]()
![]()
![]()
![]()
在△AED中,DE=![]() ,AE=1,
,AE=1,
则tan∠DAE=![]() =
=![]() ,
,
∴∠DAE=60°.
又∵OD=OA,
∴△AOD是等边三角形,
∴⊙O的半径OD=AD=2.
(3)解:∵△AOD是等边三角形,
∴∠AOD=60°.
∴![]()
![]()

练习册系列答案
相关题目