Question

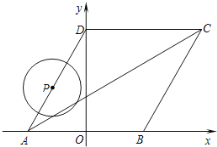
【题目】如图所示，菱形ABCD的顶点A、B在轴上，点A在点B的左侧，点D在轴的正半轴上，，点A的坐标为.

(1)求D点的坐标.

(2)求直线AC的函数关系式.

(3)动点P从点A出发，以每秒1个单位长度的速度，按照的顺序在菱形的边上匀速运动一周，设运动时间为秒.求为何值时，以点P为圆心、以1为半径的圆与对角线AC相切？

Answer 1

【答案】（1）（0，2）；（2）；（3）t=2或6或10或14

【解析】

（1）在Rt△AOD中，根据OA的长以及∠BAD的正切值，即可求得OD的长，从而得到D点的坐标；
（2）根据点A、C的坐标，利用待定系数法可求得直线AD的解析式．
（3）由于点P沿菱形的四边匀速运动一周，那么本题要分作四种情况考虑：
在Rt△OAD中，易求得AD的长，也就得到了菱形的边长，而菱形的对角线平分一组对角，那么∠DAC=∠BAC=∠BCA=∠DCA=30°；
①当点P在线段AD上时，若⊙P与AC相切，由于∠PAC=30°，那么AP=2R（R为⊙P的半径），由此可求得AP的长，即可得到t的值；
②③④的解题思路与①完全相同，只不过在求t值时，方法略有不同．

解：（1）∵点A的坐标为（-2，0），∠BAD=60°，∠AOD=90°，
∴OD=OAtan60°=2，AD=4，
∴点D的坐标为（0，2）；

（2）根据（1）知点D的坐标为（0，2）

∵AD=CD，CD∥AB，
∴C（4，2）；

设直线AC的函数表达式为y=kx+b（k≠0），
∵A（-2，0），C（4，2），

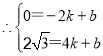
解得：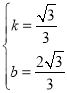

∴直线AC的解析式为；

（3）∵四边形ABCD是菱形，
∴∠DCB=∠BAD=60°，
∴∠1=∠2=∠3=∠4=30°，
AD=DC=CB=BA=4，
如图所示：

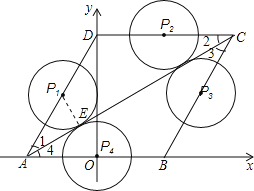
①点P在AD上与AC相切时，
连接P1E，则P1E⊥AC，P1E=r，
∵∠1=30°，
∴AP1=2r=2，
∴t1=2．
②点P在DC上与AC相切时，
CP2=2r=2，
∴AD+DP2=6，
∴t2=6．
③点P在BC上与AC相切时，
CP3=2r=2，
∴AD+DC+CP3=10，
∴t3=10．
④点P在AB上与AC相切时，
AP4=2r=2，
∴AD+DC+CB+BP4=14，
∴t4=14，
∴当t=2或6或10或14时，以点P为圆心、以1为半径的圆与对角线AC相切．

故答案为：（1）（0，2）；（2）；（3）t=2或6或10或14.