题目内容
数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线(如图1),方法如下:
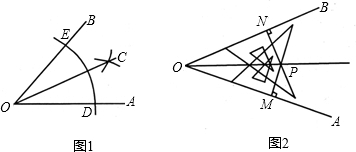
作法:
①在OA和OB上分别截取OD、OE,使OD=OE.
②分别以DE为圆心,以大于½DE的长为半径作弧,两弧在∠AOB内交于点C
③作射线OC,则OC就是∠AOB的平分线
小聪只带了直角三角板,他发现利用三角板也可以做角平分线(如图2),方法如下:
步骤:
①用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON.
②分别过M、N作OM、ON的垂线,交于点P.
③作射线OP,则OP为∠AOB的平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是 .
②小聪的作法正确吗?请说明理由.

作法:
①在OA和OB上分别截取OD、OE,使OD=OE.
②分别以DE为圆心,以大于½DE的长为半径作弧,两弧在∠AOB内交于点C
③作射线OC,则OC就是∠AOB的平分线
小聪只带了直角三角板,他发现利用三角板也可以做角平分线(如图2),方法如下:
步骤:
①用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON.
②分别过M、N作OM、ON的垂线,交于点P.
③作射线OP,则OP为∠AOB的平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是
②小聪的作法正确吗?请说明理由.
考点:作图—基本作图,全等三角形的判定
专题:
分析:①根据全等三角形的判定即可求解;
②根据HL可证Rt△OMP≌Rt△ONP,再根据全等三角形的性质即可作出判断.
②根据HL可证Rt△OMP≌Rt△ONP,再根据全等三角形的性质即可作出判断.
解答:解:①李老师用尺规作角平分线时,用到的三角形全等的判定方法SSS.
故答案为SSS;
②小聪的作法正确.
理由:∵PM⊥OM,PN⊥ON,
∴∠OMP=∠ONP=90°,
在Rt△OMP和Rt△ONP中,
,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP平分∠AOB.
故答案为SSS;
②小聪的作法正确.
理由:∵PM⊥OM,PN⊥ON,
∴∠OMP=∠ONP=90°,
在Rt△OMP和Rt△ONP中,
|
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP平分∠AOB.
点评:本题考查了用刻度尺作角平分线的方法,全等三角形的判定与性质,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列图形:①两个点;②线段;③角;④长方形;⑤两条相交直线;⑥三角形,其中一定是轴对称图形的有 ( )
| A、5个 | B、3个 | C、4个 | D、6个 |
方程(3x-2)(x-6)=3x(x-4)的解为( )
| A、-3 | B、1.5 |
| C、-1.5 | D、3 |
多项式x3y2-2x2y3+4xy4z的公因式是( )
| A、xy2 |
| B、4xy |
| C、xy2z |
| D、xyz |
已知⊙O的半径为5cm,P到圆心O的距离为6cm,则点P在⊙O( )
| A、外部 | B、内部 | C、上 | D、不能确定 |
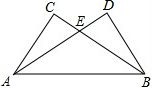 如图所示,CE=DE,EA=EB,CA=DB,求证:△ABC≌△BAD.
如图所示,CE=DE,EA=EB,CA=DB,求证:△ABC≌△BAD.