题目内容
将抛物线y=2（x-1）2+4，绕着它的顶点旋转180°，旋转后的抛物线表达式是 ．
考点：二次函数图象与几何变换
专题：计算题
分析：根据旋转的性质，把抛物线绕着它的顶点旋转180°，只是改变了抛物线的开口方向，所以可根据顶点式写出旋转后的抛物线解析式．
解答：解：∵抛物线y=2（x-1）2+4，绕着它的顶点旋转180°，
∴旋转后的抛物线的顶点坐标不变，只是开口方向改变，
∴旋转后的抛物线表达式为y=-2（x-1）2+4．
故答案为y=-2（x-1）2+4．
∴旋转后的抛物线的顶点坐标不变，只是开口方向改变，
∴旋转后的抛物线表达式为y=-2（x-1）2+4．
故答案为y=-2（x-1）2+4．
点评：本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
相关题目
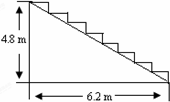遂昌元立大酒店在重新装修后，准备在大厅的主梯上铺设某种红色地毯，已知这种地毯每平方米售价30元，主楼道宽2m，其侧面如图所示，则购买地毯至少需要在同圆中，若AB和CD都是劣弧，且AB=2CD，那么弦AB和CD的大小关系是（ ）
| A、AB=2CD |
| B、AB＞2CD |
| C、AB＜2CD |
| D、无法比较它们的大小 |
