题目内容
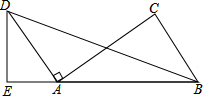如图，点E、A、B在同一直线上，AD∥BC，AB=| 3 |
| 3 |
（1）求证：△ABC∽△DAE；
（2）若∠CAD=90°，AD=BC，AE=1，求BD的长．
考点：相似三角形的判定与性质
专题：
分析：（1）利用相似三角形的判定（两边成比例，切夹角相等，两三角形相似）得出即可；
（2）利用平行线的性质得出∠C的度数，进而得出∠E的度数，再利用勾股定理得出DE，AB的长，进而求出BD的长．
（2）利用平行线的性质得出∠C的度数，进而得出∠E的度数，再利用勾股定理得出DE，AB的长，进而求出BD的长．
解答：（1）证明：∵AD∥BC，
∴∠EAD=∠ABC，
∵AB=
AD，BC=
AE，
∴
=
=
，
∴△ABC∽△DAE；
（2）解：∵∠CAD=90°，AD∥BC，
∴∠C=∠DAC=90°，
∵△ABC∽△DAE，
∴∠DEA=90°，
∵AD=BC，AE=1，AB=
AD，BC=
AE，
∴AD=BC=
，AB=3，
∴DE=
=
，BE=AE+AB=1+3=4，
∴BD=
=3
．
∴∠EAD=∠ABC，
∵AB=
| 3 |
| 3 |
∴
| AB |
| AD |
| BC |
| AE |
| 3 |
∴△ABC∽△DAE；
（2）解：∵∠CAD=90°，AD∥BC，
∴∠C=∠DAC=90°，
∵△ABC∽△DAE，
∴∠DEA=90°，
∵AD=BC，AE=1，AB=
| 3 |
| 3 |
∴AD=BC=
| 3 |
∴DE=
| 3-1 |
| 2 |
∴BD=
| 16+2 |
| 2 |
点评：此题主要考查了相似三角形的判定与性质以及勾股定理等知识，得出△ABC∽△DAE是解题关键．
练习册系列答案
相关题目
如图是一局围棋比赛的几手棋．为记录棋谱方便，横线用数字表示，纵线用字母表示，这样，黑棋
的位置可记为（B，2），白棋②的位置可记为（D，1），则白棋⑨的位置应记为（ ）| A、（C，5） |
| B、（C，4） |
| C、（4，C） |
| D、（5，C） |
如图，某考古队为进行研究，寻找一座古城遗址．根据资料记载，该城在森林附近，到两条河岸的距离相等，到古塔的距离是3 000m．根据这些资料，考古队很快找到了这座古城的遗址．你能运用学过的知识在图中合理地标出古城遗址的位置吗？请你试一试．（比例尺为1：100 000）