题目内容
14.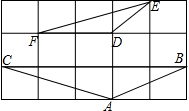 如图,方格纸上每个小正方形的边长都为1,则△ABC与△DEF相似(填全等,相似,位似,不相似),∠BAC的度数为135°.
如图,方格纸上每个小正方形的边长都为1,则△ABC与△DEF相似(填全等,相似,位似,不相似),∠BAC的度数为135°.
分析 由勾股定理求出AB=$\sqrt{5}$,AC=$\sqrt{10}$,DE=$\sqrt{2}$,EF=$\sqrt{10}$,证出$\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}$,得出△ABC∽△DEF;得出对应角相等∠BAC=∠EDF=135°即可.
解答 解:由题意得:BC=5,DF=2,
由勾股定理得:
AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
DE=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,EF=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∵$\frac{AB}{DE}=\frac{\sqrt{5}}{\sqrt{2}}=\frac{\sqrt{10}}{2}$,$\frac{AC}{DF}=\frac{\sqrt{10}}{2}$,$\frac{BC}{EF}=\frac{5}{\sqrt{10}}$=$\frac{\sqrt{10}}{2}$,
∴$\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}$,
∴△ABC∽△DEF;
∴∠BAC=∠EDF=180°-45°=135°.
故答案为:相似,135°.
点评 本题考查了相似三角形的判定与性质、勾股定理;熟练掌握勾股定理,证明三边长成比例得出三角形相似是解决问题的关键.

练习册系列答案
相关题目
 如图的六边形是正六边形,求∠BAC的大小.
如图的六边形是正六边形,求∠BAC的大小.