题目内容
9.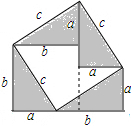 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来证明a2+b2=c2.(请你写出证明过程)
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来证明a2+b2=c2.(请你写出证明过程)
分析 根据S五边形面积=S梯形面积1+S梯形面积2=S正方形面积+2S直角三角形面积即可求解.
解答 证明:∵S五边形面积=S梯形面积1+S梯形面积2=S正方形面积+2S直角三角形面积,
即:$\frac{1}{2}(b+a+b)•b+\frac{1}{2}(a+a+b)•a={c}^{2}+2×\frac{1}{2}ab$,
即$\frac{1}{2}ab+{b}^{2}+{a}^{2}+\frac{1}{2}ab={c}^{2}+ab$,
即:a2+b2=c2.
点评 本题考查了用数形结合来证明勾股定理,证明勾股定理常用的方法是利用面积证明,本题锻炼了同学们数形结合的思想方法.

练习册系列答案
相关题目
19.下列式子是分式的是( )
| A. | $\frac{x}{2}$ | B. | $\frac{3}{x+1}$ | C. | $\frac{x}{2}+y$ | D. | $\frac{x}{π}$ |
20.若∠1=37°18′,则∠1的补角度数为( )
| A. | 52°42′ | B. | 53°42′ | C. | 142°42′ | D. | 163°42′ |
17.下列计算结果正确的是( )
| A. | $\sqrt{{{(-3)}^2}}=3$ | B. | $\sqrt{36}$=±6 | C. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | D. | $3+2\sqrt{3}=5\sqrt{3}$ |
14.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.给出下列说法:①抛物线的对称轴是直线x=1;②抛物线一定经过点(3,0);③在对称轴左侧,y随x增大而减小;④若A(-$\frac{3}{4}$,y1)、B($\frac{7}{5}$,y2)两点在此抛物线上,则y1>y2.上述说法正确的个数有( )
| x | … | -3 | -2 | -1 | 1 | 2 | … |
| y | … | -6 | 0 | 4 | 6 | 4 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1. 如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )
如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )
 如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )
如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |