题目内容
8.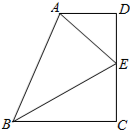 如图,已知四边形ABCD中,∠C=∠D=90°,AE平分∠DAB,BE平分∠ABC,且E在D上.
如图,已知四边形ABCD中,∠C=∠D=90°,AE平分∠DAB,BE平分∠ABC,且E在D上.(1)求∠AEB;
(2)求证:DE=CE.
分析 (1)延长AE、BC交于点M,求出∠DAE=∠CME,AB=BM,根据ASA推出△ADE≌△MCE,根据全等得出AE=EM,∠DAE=∠M,求出∠M=∠BAE,推出AB=BM,根据等腰三角形的性质得出即可;
(2)过E作EF⊥AB于F,根据角平分线性质得出EF=DE,EF=CE即可.
解答 (1)解:延长AE、BC交于点M,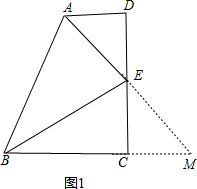
∵AD∥BC
∴∠DAE=∠CME,
∵AE平分∠BAD,
∴∠DAE=∠BAM,
∴∠BAM=∠CME,
∴AB=BM,
在△ADE和△MCE中,
$\left\{\begin{array}{l}{∠D=∠ECM}\\{DE=CE}\\{∠AED=∠CEM}\end{array}\right.$,
∴△ADE≌△MCE,
∴AE=EM,∠DAE=∠M
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠M=∠BAE,
∴AB=BM,
∵AE=EM,
∴BE⊥AM,
∴∠AEB=90°;
(2)证明:如图2,过E作EF⊥AB于F,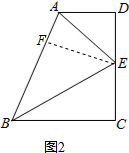
∵∠D=∠C=90°,AE平分∠BAD,BE平分∠ABC
∴EF=DE=CE,
即DE=CE.
点评 本题主要考查了全等三角形的判定与性质,角平分线性质,及等腰三角形的性质的应用,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具,能灵活运用性质进行推理是解此题的关键,注意:角平分线上的点到角的两边的距离相等.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
18.某工厂工人的工作时间为每月25天,每天8小时,每名工人每月有基本工资400元.该厂生产A、B两种产品,工人每生产一件A种产品,可得到报酬0.75元;每生产一件B种产品,可得到报酬1.40元,如表记录了工人小王的工作情况:
(1)求小王每生产一件A种产品和一件B种产品,分别需要多少时间?
(2)求小王每月工资额范围.
| 生产A种产品件数 | 生产B种产品件数 | 合计用工时间(分钟) |
| 1 | 1 | 35 |
| 3 | 2 | 85 |
(2)求小王每月工资额范围.
16.直角三角形一边长为4,斜边长5,则面积为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
13.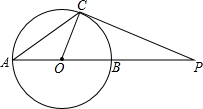 如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )
如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )
 如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )
如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )| A. | 40° | B. | 35° | C. | 30° | D. | 25° |
