题目内容
20.已知抛物线y=x2-2x+1.(1)求它的对称轴和顶点坐标;
(2)根据图象,确定当x>2时,y的取值范围.
分析 (1)把抛物线解析式化为顶点式即可得出对称轴和顶点坐标;
(2)利用描点法画出图象,根据图象利用数形结合的方法确定当x>2时,y的取值范围即可.
解答 解:(1)y=x2-2x+1=(x-1)2,
对称轴为直线x=1,顶点坐标为(1,0);
(2)抛物线图象如下图所示:
由图象可知当x>2时,y的取值范围是y>1.
点评 本题考查了二次函数的性质,解题的关键是确定对称轴及顶点坐标并作出图象.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
15.下列叙述正确的是( )
| A. | 任意两个正方形一定是相似的 | B. | 任意两个矩形一定是相似的 | ||
| C. | 任意两个菱形一定是相似的 | D. | 任意两个等腰梯形一定是相似的 |
5.抛一枚质地均匀的正六面体骰子,落地后向上一面的点数是2的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
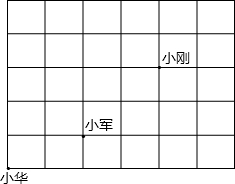 课间操时小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以用坐标表示成(4,3).
课间操时小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以用坐标表示成(4,3).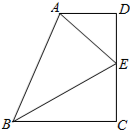 如图,已知四边形ABCD中,∠C=∠D=90°,AE平分∠DAB,BE平分∠ABC,且E在D上.
如图,已知四边形ABCD中,∠C=∠D=90°,AE平分∠DAB,BE平分∠ABC,且E在D上.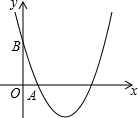 如图,已知二次函数y=x2+bx+c的图象分别经过点A(1,0),B(0,3).
如图,已知二次函数y=x2+bx+c的图象分别经过点A(1,0),B(0,3).