题目内容
 如图,在正方形ABCD中,E、F分别为BC、AB上的点,且∠FED=90°,∠DFE=60°,若正方形边长为1,求△DEF的面积.
如图,在正方形ABCD中,E、F分别为BC、AB上的点,且∠FED=90°,∠DFE=60°,若正方形边长为1,求△DEF的面积.考点:正方形的性质,相似三角形的判定与性质
专题:
分析:根据等角的余角相等求出∠BEF=∠CDE,再根据两组角对应相等,两三角形相似可得△BFE和△CED相似,解直角三角形求出
=
,再根据相似三角形对应边成比例求出BE,然后求出CE,利用勾股定理列式求出DE2,然后根据三角形的面积公式列式计算即可得解.
| EF |
| DE |
| ||
| 3 |
解答:解:∵∠FED=90°,
∴∠BEF+∠CED=∠CDE+∠CED=90°,
∴∠BEF=∠CDE,
又∵∠B=∠C=90°,
∴△BFE∽△CED,
∵∠FED=90°,∠DFE=60°,
∴
=
,
∵△BFE∽△CED,
∴
=
=
,
∴BE=
CD=
,
∴CE=1-
,
在Rt△CDE中,DE2=CE2+CD2=(1-
)2+12=
,
∵EF=
•DE,
∴△DEF的面积=
DE•EF=
•DE•
•DE=
×
=
.
∴∠BEF+∠CED=∠CDE+∠CED=90°,
∴∠BEF=∠CDE,
又∵∠B=∠C=90°,
∴△BFE∽△CED,
∵∠FED=90°,∠DFE=60°,
∴
| EF |
| DE |
| ||
| 3 |
∵△BFE∽△CED,
∴
| BE |
| CD |
| EF |
| DE |
| ||
| 3 |
∴BE=
| ||
| 3 |
| ||
| 3 |
∴CE=1-
| ||
| 3 |
在Rt△CDE中,DE2=CE2+CD2=(1-
| ||
| 3 |
7-2
| ||
| 3 |
∵EF=
| ||
| 3 |
∴△DEF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
7-2
| ||
| 3 |
7
| ||
| 18 |
点评:本题考查了正方形的性质,同角的余角相等的性质,相似三角形的判定与性质,解直角三角形,难点在于求出DE2并用DE2表示出△DEF的面积.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
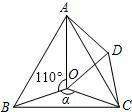 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.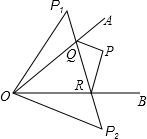 如图所示,∠AOB=45°,角内有一点P,P1、P2分别是点P关于两边OA和OB的对称点,连P1P2与角两边交于Q、R.
如图所示,∠AOB=45°,角内有一点P,P1、P2分别是点P关于两边OA和OB的对称点,连P1P2与角两边交于Q、R.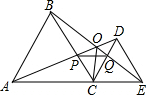 如图,C为AE上一点,在AE同侧分别作等边△ABC和等边△CDE,AD与BC交于点P,BE与CD交于Q,连接PQ.求证:∠AOB=60°.
如图,C为AE上一点,在AE同侧分别作等边△ABC和等边△CDE,AD与BC交于点P,BE与CD交于Q,连接PQ.求证:∠AOB=60°. 操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a、b、c(如图①),分别用4张这样的直角三角形纸片拼成如图②③的形状,图②中的两个小正方形的面积S2、S3与图③中小正方形的面积S1有什么关系?你能得到a、b、c之间有什么关系?
操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a、b、c(如图①),分别用4张这样的直角三角形纸片拼成如图②③的形状,图②中的两个小正方形的面积S2、S3与图③中小正方形的面积S1有什么关系?你能得到a、b、c之间有什么关系?