题目内容
5.先化简,再求值:($\frac{m}{m-2}$-$\frac{2m}{m^2-4}$)÷$\frac{m}{m+2}$,请在2,-2,0,3当中选一个合适的数代入求值.分析 先化简分式,然后根据分式有意义的条件即可求出m的值,从而可求出原式的值.
解答 解:原式=($\frac{m}{m-2}$-$\frac{2m}{(m-2)(m+2)}$)×$\frac{m+2}{m}$
=$\frac{m}{m-2}$×$\frac{m+2}{m}$-$\frac{2m}{(m-2)(m+2)}$×$\frac{m+2}{m}$
=$\frac{m+2}{m-2}$-$\frac{2}{m-2}$
=$\frac{m}{m-2}$,
∵m≠±2,0,
∴当m=3时,
原式=3
点评 本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
15. 课间操时,小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(-1,-2)表示,小军的位置用(1,-1)表示,那么你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(-1,-2)表示,小军的位置用(1,-1)表示,那么你的位置可以表示成( )
 课间操时,小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(-1,-2)表示,小军的位置用(1,-1)表示,那么你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(-1,-2)表示,小军的位置用(1,-1)表示,那么你的位置可以表示成( )| A. | (4,3) | B. | (3,4) | C. | (3,1) | D. | (1,3) |
17.下列四个几何体的俯视图中与众不同的是( )
| A. |  | B. |  | C. |  | D. |  |
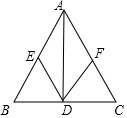 如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点. 如图所示,⊙I是Rt△ABC的内切圆,点D、E、F分别是且点,若∠ACB=90°,AB=5cm,BC=4cm,则⊙I的周长为2πcm.
如图所示,⊙I是Rt△ABC的内切圆,点D、E、F分别是且点,若∠ACB=90°,AB=5cm,BC=4cm,则⊙I的周长为2πcm.