题目内容
12.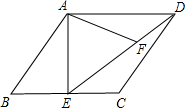 如图,在菱形ABCD中,过点A作AE⊥BC,垂足E为BC中点,连接DE,F为DE上一点,且∠AFE=∠B.
如图,在菱形ABCD中,过点A作AE⊥BC,垂足E为BC中点,连接DE,F为DE上一点,且∠AFE=∠B.(1)求证:△ADF∽△DEC;
(2)若AB=2,求AF的长.
分析 (1)由菱形的性质得出AD∥BC,AB∥CD,得出∠ADF=∠DEC,∠B+∠C=180°,再由已知条件和邻补角关系求出∠AFD=∠C,即可得出结论;
(2)由菱形的性质得出AD=AB=BC=2,由勾股定理求出AE、DE,再由相似三角形的性质得出对应边成比例,即可求出AF的长.
解答 (1)证明:∵四边形ABCD是菱形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠DEC,∠B+∠C=180°,
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)解:∵四边形ABCD是菱形,
∴AD=AB=BC=2,
∵AE⊥BC,E为BC中点,
∴AE⊥AD,BE=$\frac{1}{2}$BC=1,
∴∠DAE=90°,AE=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴DE=$\sqrt{A{E}^{2}+A{D}^{2}}$=$\sqrt{7}$,
∵△ADF∽△DEC,
∴$\frac{AF}{CD}=\frac{AD}{DE}$,
即$\frac{AF}{2}=\frac{2}{\sqrt{7}}$,
解得:AF=$\frac{4\sqrt{7}}{7}$.
点评 本题考查了菱形的性质、相似三角形的判定与性质、勾股定理;熟练掌握菱形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.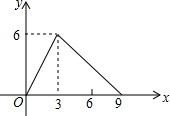 如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )
如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )
 如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )
如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
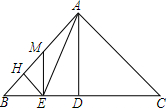 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,EH⊥AB,垂足是H.在AB上取一点M,使BM=2DE,连接ME.求证:ME⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,EH⊥AB,垂足是H.在AB上取一点M,使BM=2DE,连接ME.求证:ME⊥BC.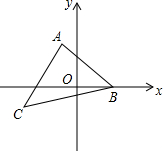 如图,已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1)
如图,已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1)