题目内容
20.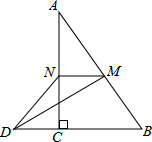 如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD.连接DM、DN、MN.若AB=6,求DN的长.
如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD.连接DM、DN、MN.若AB=6,求DN的长.
分析 连接CM,根据直角三角形的性质求出CM,根据三角形中位线定理得到MN=$\frac{1}{2}$BC,MN∥BC,证明四边形NDCM是平行四边形,根据平行四边形的性质解答.
解答 解:连接CM,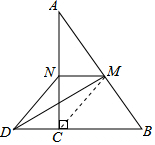
∵∠ACB=90°,M是AB的中点,
∴CM=$\frac{1}{2}$AB=3,
∵M、N分别是AB、AC的中点,
∴MN=$\frac{1}{2}$BC,MN∥BC,
∵CD=$\frac{1}{3}$BD,
∴MN=CD,又MN∥BC,
∴四边形NDCM是平行四边形,
∴DN=CM=3.
点评 本题考查的是直角三角形的性质和三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
11.计算正确的是( )
| A. | 3.4×104=340000 | B. | m×2m2=3m2 | C. | (-$\frac{1}{2}$mn2)2=m2n4 | D. | 4xy-4yx=0 |
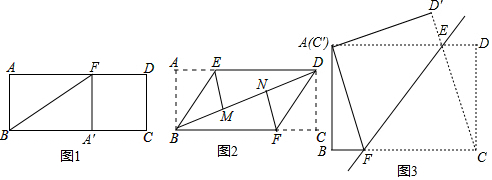
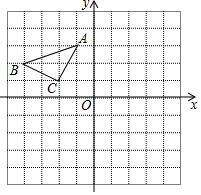 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.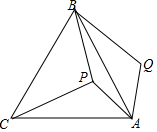 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=150°.
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=150°.