题目内容
4．
已知抛物线y=ax2+bx+c的形状与抛物线y=-x2的形状完全相同、开口方向相反，且经过点（-1，4）、（2，4）．（1）求这个函数的关系式．
（2）在右边格点中，利用直角坐标系中画出它的图象．
（3）根据图象说明：当x为何值时，y＞0；当x为何值时，y＜0．
分析 （1）利用抛物线与抛物线y=-x2的形状完全相同、开口方向相反得到a=1，再把点（-1，4）、（2，4）代入y=ax2+bx+c，这样得到关于a、b、c的方程组，然后解方程求出a、b、c的值即可；
（2）利用描点点画函数图象；
（3）观察图象可确定x的范围．
解答 解：（1）根据题意得$\left\{\begin{array}{l}{a=1}\\{a-b+c=4}\\{4a+2b+c=4}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=1}\\{b=-1}\\{c=2}\end{array}\right.$，
所以抛物线解析式为y=x2-x+2；
（2）y=x2-x+2=（x-$\frac{1}{2}$）2+$\frac{7}{4}$，抛物线的顶点坐标为（$\frac{1}{2}$，$\frac{7}{4}$）
如图，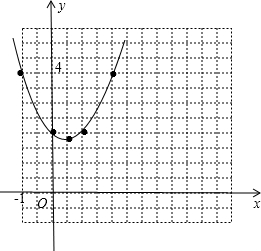
（2）无论x取何值，y＞0．
点评 本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．也考查了二次函数的性质．
练习册系列答案
相关题目
9．下列方程组中，是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{x+2y=1}\\{3y-z=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{2x+3y=5}\\{x-y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x+y=2}\\{xy=-3}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{y=3x-2}\\{\frac{2}{x}-1=0}\end{array}\right.$ |
16．我省公布的居民用电电价听证方案如下：
例：某户月用电量400度，则需缴电费为210×0.55+（350-210）×（0.55+0.05）+（400-350）×（0.55+0.15）=234.5（元）．
（1）如果按此方案计算，小华家5月份的电费为139.5元，请你求出小华家5月份的用电量；
（2）依据方案请你回答：若小华家某月的电费为248元，则小华家该月用电量是多少？属于第几档？
| 第一档电量 | 第二档电量 | 第三档电量 |
| 月用电量210度以下，每度价格0.55元 | 月用电量210度至350度，每度比第一档提价0.05元 | 月用电量350度以上，每度比第一档提价格0.15元 |
（1）如果按此方案计算，小华家5月份的电费为139.5元，请你求出小华家5月份的用电量；
（2）依据方案请你回答：若小华家某月的电费为248元，则小华家该月用电量是多少？属于第几档？