题目内容
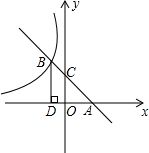 如图所示,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数y=-
如图所示,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数y=-| 8 |
| x |
(1)求直线AB的解析式;
(2)若点P是线段BD上一点,且△PBC的面积等于3,求点P的坐标.
考点:反比例函数与一次函数的交点问题
专题:待定系数法
分析:(1)根据图象上的点满足函数解析式,可得B点坐标,根据待定系数法,可得函数解析式;
(2)三角形的面积公式,BP的长,可得P点坐标.
(2)三角形的面积公式,BP的长,可得P点坐标.
解答:解:(1)OD=2,B点的横坐标是-2,
当x=-2时,y=-
=4,
∴B点坐标是(-2,4),
设直线AB的解析式是y=kx+b,图象过(-2,4)、(0,2),
,
解得
,
∴直线AB的解析式为y=-x+2;
(2)∵OD=2,S△OBP=
BP•OD=3,
∴BP=3,
PD=BD-BP=4-3=1,
∴P点坐标是(-2,1).
当x=-2时,y=-
| 8 |
| -2 |
∴B点坐标是(-2,4),
设直线AB的解析式是y=kx+b,图象过(-2,4)、(0,2),
|
解得
|
∴直线AB的解析式为y=-x+2;
(2)∵OD=2,S△OBP=
| 1 |
| 2 |
∴BP=3,
PD=BD-BP=4-3=1,
∴P点坐标是(-2,1).
点评:本题考查了反比例函数与一函数的交点问题,待定系数法求函数解析式的关键.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题: 在△ABC中,AD是BC边上的高,∠C=45°,sinB=
在△ABC中,AD是BC边上的高,∠C=45°,sinB=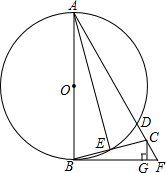 如图,AB为⊙O的直径,BF切⊙O于点B,AF交⊙O于点D,点C在DF上,BC交⊙O于点E,且∠BAF=2∠CBF,CG⊥BF于点G,连接AE.
如图,AB为⊙O的直径,BF切⊙O于点B,AF交⊙O于点D,点C在DF上,BC交⊙O于点E,且∠BAF=2∠CBF,CG⊥BF于点G,连接AE.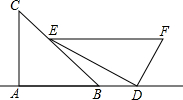 小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,其中A,B,D在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠F=60°,量得DF=6,求BD的长.
小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,其中A,B,D在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠F=60°,量得DF=6,求BD的长. 如图,△ABC中,∠A=40°,AB的垂直平分线MN交AC于点D,∠DBC=30°,若AB=m,BC=n,则△DBC的周长为
如图,△ABC中,∠A=40°,AB的垂直平分线MN交AC于点D,∠DBC=30°,若AB=m,BC=n,则△DBC的周长为 如图,在四边形ABCD中,AD∥BC,AB=CD=2,BC=5,∠BAD的平分线交BC于点E,且AE∥CD,则四边形ABCD的面积为
如图,在四边形ABCD中,AD∥BC,AB=CD=2,BC=5,∠BAD的平分线交BC于点E,且AE∥CD,则四边形ABCD的面积为