题目内容
19.在一个不透明的袋子中,放入了2个红球和m个白球,已知从中摸出一个球是红球的概率为0.4.(1)求m的值;
(2)如果从中一次摸出2个球,求至少有一个是红球的概率,请用画树状图或列表的方法进行分析.
分析 (1)由概率公式可列方程:$\frac{2}{2+m}$=0.4,解此方程即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与至少有一个是红球的情况,再利用概率公式求解即可求得答案.
解答 解:(1)根据题意得:$\frac{2}{2+m}$=0.4,
解得:m=3;
经检验:x=3是原分式方程的解;
∴m的值为3;
(2)画树状图得: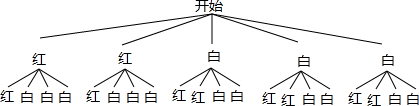
∵共有20种等可能的结果,至少有一个是红球的有14种情况,
∴至少有一个是红球的概率为:$\frac{14}{20}$=$\frac{7}{10}$.
点评 此题考查了列表法或树状图法求概率.注意掌握方程思想的应用,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
10.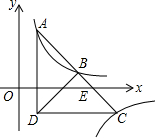 如图,Rt△ADC在平面直角坐标系下如图放置,斜边AC交x轴于点E,过点A的双曲线y=$\frac{k}{x}$(m≠0)交Rt△ADC斜边AC的中点B,连接BD,过点C作双曲线y=$\frac{m}{x}$(m≠0).若BD=3BE,A的坐标为(1,8),则m=( )
如图,Rt△ADC在平面直角坐标系下如图放置,斜边AC交x轴于点E,过点A的双曲线y=$\frac{k}{x}$(m≠0)交Rt△ADC斜边AC的中点B,连接BD,过点C作双曲线y=$\frac{m}{x}$(m≠0).若BD=3BE,A的坐标为(1,8),则m=( )
 如图,Rt△ADC在平面直角坐标系下如图放置,斜边AC交x轴于点E,过点A的双曲线y=$\frac{k}{x}$(m≠0)交Rt△ADC斜边AC的中点B,连接BD,过点C作双曲线y=$\frac{m}{x}$(m≠0).若BD=3BE,A的坐标为(1,8),则m=( )
如图,Rt△ADC在平面直角坐标系下如图放置,斜边AC交x轴于点E,过点A的双曲线y=$\frac{k}{x}$(m≠0)交Rt△ADC斜边AC的中点B,连接BD,过点C作双曲线y=$\frac{m}{x}$(m≠0).若BD=3BE,A的坐标为(1,8),则m=( )| A. | -8 | B. | -18 | C. | -28 | D. | -48 |
14.2015年全国两会民生话题成为社会焦点,临沂市记者为了了解百胜“两会民生话题”的聚集点,随机调查了临沂市部分市民,并对调查结果进行了整理,绘制了如图所示的不完整的统计图表.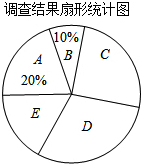
请根据图表中提供的信息解答下列问题:
(1)填空:m=40,n=100.扇形统计图中E组所占的百分比为15%;
(2)临沂市现有人口大约1100万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?

| 组别 | 焦点话题 | 频数(人数) |
| A | 食品安全 | 80 |
| B | 教育医疗 | m |
| C | 就业养老 | n |
| D | 生态环保 | 120 |
| E | 其他 | 60 |
(1)填空:m=40,n=100.扇形统计图中E组所占的百分比为15%;
(2)临沂市现有人口大约1100万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
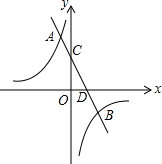 如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-1,6)和点B(3,m),与y轴交于点C,与x轴交于点D.
如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-1,6)和点B(3,m),与y轴交于点C,与x轴交于点D.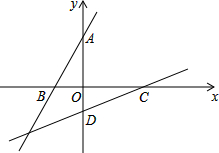 已知A、B、C、D是平面坐标系中坐标轴上的点,且△AOB≌△COD.设直线AB的表达式为y1=k1x+b1,直线CD的表达式为y2=k2x+b2,则k1•k2=1.
已知A、B、C、D是平面坐标系中坐标轴上的点,且△AOB≌△COD.设直线AB的表达式为y1=k1x+b1,直线CD的表达式为y2=k2x+b2,则k1•k2=1.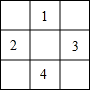 如图,将一块正方形地面等分成9块,其中标有1、2、3、4四个小方格是空地,另外五个小方格是草坪,一只自由飞行的小乌,随意地落在方格地面上,则小鸟落在草坪上的概率是$\frac{5}{9}$.
如图,将一块正方形地面等分成9块,其中标有1、2、3、4四个小方格是空地,另外五个小方格是草坪,一只自由飞行的小乌,随意地落在方格地面上,则小鸟落在草坪上的概率是$\frac{5}{9}$.