题目内容
已知:关于x的一元二次方程:kx2+2(k+1)x+k=0有两个实数根,求k的取值范围.
考点:根的判别式
专题:
分析:若一元二次方程有两个实数根,则根的判别式△=b2-4ac≥0,建立关于k的不等式,求出k的取值范围.还要注意二次项系数不为0.
解答:解:∵方程有两个实数根,
∴根的判别式△=b2-4ac=4(k+1)2-4k2=8k+4≥0,
即k≥-
,
又∵k≠0,
∴k≥-
且k≠0.
∴根的判别式△=b2-4ac=4(k+1)2-4k2=8k+4≥0,
即k≥-
| 1 |
| 2 |
又∵k≠0,
∴k≥-
| 1 |
| 2 |
点评:本题考查了一元二次方程根的判别式的应用.切记不要忽略一元二次方程二次项系数不为零这一隐含条件.

练习册系列答案
相关题目
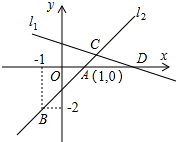 如图,直线l1的解析表达式为y=-
如图,直线l1的解析表达式为y=- 在△ABC中,∠A=
在△ABC中,∠A= 如图,已知线段AB=10cm,AP=6cm,P是OB的中点,则A0=
如图,已知线段AB=10cm,AP=6cm,P是OB的中点,则A0=