题目内容
因式分解:(k+1)x2+(3k+1)x+2k-2= .
考点:因式分解-十字相乘法等
专题:计算题
分析:原式利用十字相乘法分解即可.
解答:解:原式=[(k+1)x-k+1](x-2).
故答案为:[(k+1)x-k+1](x-2).
故答案为:[(k+1)x-k+1](x-2).
点评:此题考查了因式分解-十字相乘法,熟练掌握十字相乘的方法是解本题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
下列方程中,两个实数根的和为4的是( )
| A、x2-4x-1=0 |
| B、x2+4x-l=0 |
| C、x2-8x+4=0 |
| D、x2-4x+5=0 |
 如图,AB,CD为⊙O互相垂直的直径,P为
如图,AB,CD为⊙O互相垂直的直径,P为
 如图,点A、B、C都在方格纸的格点上,请你再找一个格点D,使点A、B、C、D组成一个轴对称图形.这样的点D最多能找到
如图,点A、B、C都在方格纸的格点上,请你再找一个格点D,使点A、B、C、D组成一个轴对称图形.这样的点D最多能找到 如图,在平面直角坐标系xOy中,A(4,4)、B(1,2)、C(3,2).若△ABC与△DBC全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(4,4)、B(1,2)、C(3,2).若△ABC与△DBC全等,则点D坐标为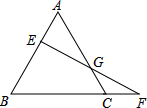 已知:△ABC是等边三角形,点E在AB边上运动,EF交AC于G,交BC的延长线于F,且AE=CF.
已知:△ABC是等边三角形,点E在AB边上运动,EF交AC于G,交BC的延长线于F,且AE=CF.