题目内容
一个三角形三边长的比为3：4：5，它的周长是60cm，这个三角形最大边上的中线长是 ．
考点：勾股定理的逆定理
专题：
分析：由条件可求得三角形的三边，且满足勾股定理的逆定理，可知该三角形为直角三角形，斜边为25，可知其斜边上的中线等于斜边的一半可得答案．
解答：解：
∵三角形三边长的比为3：4：5，它的周长是60cm，
∴三角形的三边分别为15cm、20cm、25cm，
∵152+202=225+400=625=252，
∴该三角形为直角三角形，斜边为25cm，
∴斜边上的中线长为12.5cm，
故答案为：12.5cm．
∵三角形三边长的比为3：4：5，它的周长是60cm，
∴三角形的三边分别为15cm、20cm、25cm，
∵152+202=225+400=625=252，
∴该三角形为直角三角形，斜边为25cm，
∴斜边上的中线长为12.5cm，
故答案为：12.5cm．
点评：本题主要考查勾股定理的逆定理及直角三角形的性质，由条件求得三角形的三边判断出该三角形为直角三角形是解题的关键．
练习册系列答案
相关题目
如图，数轴上与1、以下计算正确的是（ ）
| A、3a2•4ab=7a3b |
| B、（2ab3）•（-4ab）=-2a2b4 |
| C、（xy）3•（-x2y）=-x3y3 |
| D、-3a2b（-3ab）=9a3b2 |
如图，菱形ABCD中，∠ABC=120°，AB=4，E是BC边的中点，点P在对角线AC上，连接BP，EP，则△BPE周长最小值为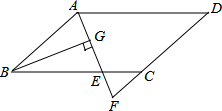
如图，在?ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，若BG=4，则△CEF的面积是（ ）