题目内容
 如图,AB,CD为⊙O互相垂直的直径,P为
如图,AB,CD为⊙O互相垂直的直径,P为 |
| BC |
考点:圆周角定理,相似三角形的判定与性质
专题:证明题
分析:首先连接AD,PB,BD,由AB,CD为⊙O互相垂直的直径,易证得△ADE∽△APD,△APF∽△DPB,然后由相似三角形的对应边成比例,可证得AD:DE=AF:DB,继而可得AF•DE=AD•DB=
OA•
OA=2OA2.
| 2 |
| 2 |
解答: 证明:连结AD,PB,BD,
证明:连结AD,PB,BD,
∵AB,CD为⊙O互相垂直的直径,
∴∠ADE=
∠AOC=90°,∠APD=
∠AOD=45°,
∴∠ADE=∠APD,
∵∠EAD=∠DAP,
∴△ADE∽△APD,
∴DE:PD=AD:AP,
∴AP:PD=AD:DE,
∵∠APF=∠DPB=45°,∠PAF=∠PDB,
∴△APF∽△DPB,
∴AF:DB=AP:PD,
∴AD:DE=AF:DB,
∴AF•DE=AD•DB=
OA•
OA=2OA2.
∴AF•DE为一定值.
 证明:连结AD,PB,BD,
证明:连结AD,PB,BD,∵AB,CD为⊙O互相垂直的直径,
∴∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ADE=∠APD,
∵∠EAD=∠DAP,
∴△ADE∽△APD,
∴DE:PD=AD:AP,
∴AP:PD=AD:DE,
∵∠APF=∠DPB=45°,∠PAF=∠PDB,
∴△APF∽△DPB,
∴AF:DB=AP:PD,
∴AD:DE=AF:DB,
∴AF•DE=AD•DB=
| 2 |
| 2 |
∴AF•DE为一定值.
点评:此题考查了圆周角定理以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列结论正确的是( )
| A、a一定是正数 |
| B、倒数等于它本身的数只有1 |
| C、面积为2的正方形的边长a是无理数 |
| D、0是最小的整数 |
如果ab=-1,n=2012,那么an•bn的值为( )
| A、-2012 | B、2012 |
| C、1 | D、-1 |
 如图,数轴上与1、
如图,数轴上与1、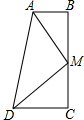 已知,如图∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
已知,如图∠B=∠C=90°,M是BC的中点,DM平分∠ADC.