Question

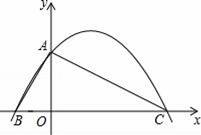
已知直线l分别与x轴、y轴交于A、B两点，与双曲线y=（m≠0，x＞0）分别交于D、E两点，若点D的坐标为（4，1），点E的坐标为（1，n）

（1）分别求出直线l与双曲线的解析式；

（2）求△EOD的面积．

Answer 1

【考点】反比例函数与一次函数的交点问题．

【专题】计算题．

【分析】（1）只需运用待定系数法就可求出反比例函数的解析式，把点E的坐标代入反比例函数的解析式，就可求出点E的坐标，然后运用待定系数法就可求出直线l的解析式；

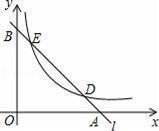
（2）连接OD、OE，过点D作DM⊥OA于M，作EN⊥OA于N，如图，只需运用割补法，就可求出△EOD的面积．

【解答】解：（1）把D（4，1）代入反比例函数的解析式得，

m=4×1=4，

∴反比例函数的解析式为y=．

把点E（1，n）的坐标代入y=得n=4，

∴点E的坐标为（1，4）．

设直线l的解析式为y=kx+b，

则有，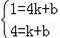

解得，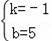

∴直线l的解析式为y=﹣x+5；

（2）连接OD、OE，过点D作DM⊥OA于M，作EN⊥OA于N，如图．

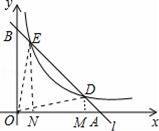
∵点A是直线y=﹣x+5与x轴的交点，

∴点A的坐标为（5，0），OA=5，

∴S_△DOE=S_△AOE﹣S_△ADO

=×5×4﹣×5×1=．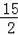

【点评】本题主要考查了运用待定系数法求一次函数和反比例函数的解析式，运用割补法是解决第（2）小题的关键．