题目内容
17．已知|2012-a|+$\sqrt{a-2014}$=a，求a-20122的值．分析 首先根据二次根式有意义的条件可得a≥2014，因此|2012-a|=a-2012，然后可得$\sqrt{a-2014}$=2012，再两边同时平方可得a-2014=20122，进而可得答案．
解答 解：由|2012-a|+$\sqrt{a-2014}$=a，得
a-2012+$\sqrt{a-2014}$=a．
$\sqrt{a-2014}$=2012，
平方，得a-2014=20122．
移项，得a-20122=2014．
点评 本题考查了二次根式有意义的条件，利用二次根式的有意义的条件化简绝对值是解题关键．
练习册系列答案
相关题目
如图，在矩形ABCD中，BE⊥AC于点E，DF⊥AC于点F，如果AE=1，EF=2，那么FC的长度是1，AB的长度是2．
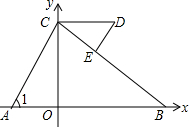如图，平面直角坐标系中，C（0，5）、D（a，5）（a＞0），A、B在x轴上，∠1=∠D，请写出∠ACB和∠BED数量关系以及证明．
如图，在正方形ABCD中，两条对角线相交于点O，∠BCA的平分线交BD于E，若正方形ABCD的周长为12cm，则BE=1cm．