题目内容
12.已知:△ABC和△DEF中,AB=DE,AC=DF,AM和DN分别是中线,且AM=DN.求证:△ABC≌△DEF.
分析 根据SAS,可得△ABM≌△A′CM(SAS),根据SSS,可得△AA′C≌△DD′F,根据SAS,可得△A′MC≌△D′NF(SAS),根据SSS,可得答案.
解答 证明:如图:
延长AM至A′,使A′M=AM,延长DN至D′,使D′N=DN,连接A′C、D′F,
∵AM是△ABC的中线,
∴BM=MC,
在△ABM和△A′CM中,
$\left\{\begin{array}{l}{BM=MC}\\{∠AMB=∠A′MC}\\{AM=A′M}\end{array}\right.$,
∴△ABM≌△A′CM(SAS),
∴AB=A′C,
同理可得DE=D′F,
∵AB=DE,
∴A′C=D′F,
∵AM=DN,AA′=2AM,DD′=2DN,
∴AA′=DD′,
在△AA′C和△DD′F中,
$\left\{\begin{array}{l}{AC=DF}\\{AA′=DD′}\\{A′C=D′F}\end{array}\right.$,
∴△AA′C≌△DD′F(SSS),
∴∠A′=∠D′,
在△A′MC和△D′NF中,
$\left\{\begin{array}{l}{A′M=D′N}\\{∠A′=∠D′}\\{A′C=D′F}\end{array}\right.$,
∴△A′MC≌△D′NF(SAS),
∴MC=NF,
∵AM、DN分别是两三角形中线,
∴BC=2MC,EF=2NF,
∴BC=EF,
在△ABC和DEF中,
$\left\{\begin{array}{l}{AB=DE}\\{AC=DF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌DEF(SSS).
点评 本题考查了全等三角形的判定与性质,利用中线的性质得出△ABM≌△A′CM是解题关键,熟记全等三角形的判定与性质并根据条件选择适当的方法证明.

| A. | 两直线平行,同旁内角互补 | B. | 两直线平行,同位角相等 | ||
| C. | 等角的补角相等 | D. | 相等的角是对顶角 |
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{10}$ | D. | $\frac{3}{10}$ |
| A. | 86×107 | B. | 8.6×109 | C. | 8.6×108 | D. | 0.86×109 |
| A. | 4 | B. | 12 | C. | 4或12 | D. | 6或8 |
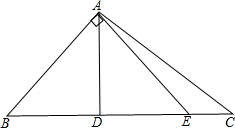 如图,在等腰直角△ABC中,AB=AC,∠BAC=90°,D、E是BC边上的点,且∠DAE=45°,试判断线段BD、DE和EC之间的数量关系,并证明你的结论.
如图,在等腰直角△ABC中,AB=AC,∠BAC=90°,D、E是BC边上的点,且∠DAE=45°,试判断线段BD、DE和EC之间的数量关系,并证明你的结论.