题目内容
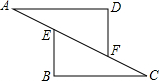 如图所示,在△AFD和△BEC中,点A,E,F,C在同一直线上,有下列四个论断中选哪三个作为条件不能证明△ADF和△BCE全等( )
如图所示,在△AFD和△BEC中,点A,E,F,C在同一直线上,有下列四个论断中选哪三个作为条件不能证明△ADF和△BCE全等( )(1)AD=CB;(2)AE=CF;(3)∠B=∠D;(4)AD∥BC.
| A、(1)(2)(3) |
| B、(1)(2)(4) |
| C、(2)(3)(4) |
| D、(1)(3)(4) |
考点:全等三角形的判定
专题:
分析:利用全等三角形的判定方法对四个选项分别证明即可.
解答:解:A、(1)AD=CB;(2)AE=CF;(3)∠B=∠D;满足的是SSA,故不能证明全等;
B、(1)AD=CB;(2)AE=CF;(4)AD∥BC,
∵AE=CF,
∴AF=CE,
∵AD∥BC,
∴∠A=∠C,
在△ADF和△CBE中,
,
∴△ADF≌△CBE(SAS);
故B可以证明;
C、(2)AE=CF;(3)∠B=∠D;(4)AD∥BC;
∵AE=CF,
∴AF=CE,
∵AD∥BC,
∴∠A=∠C,
在△ADF和△CBE中,
,
∴△ADF≌△CBE(AAS);
故C可以证明;
D、(1)AD=CB;(3)∠B=∠D;(4)AD∥BC.
∵AD∥BC,
∴∠A=∠C,
在△ADF和△CBE中,
,
∴△ADF≌△CBE(ASA);
故D可以证明;
故选A.
B、(1)AD=CB;(2)AE=CF;(4)AD∥BC,
∵AE=CF,
∴AF=CE,
∵AD∥BC,
∴∠A=∠C,
在△ADF和△CBE中,
|
∴△ADF≌△CBE(SAS);
故B可以证明;
C、(2)AE=CF;(3)∠B=∠D;(4)AD∥BC;
∵AE=CF,
∴AF=CE,
∵AD∥BC,
∴∠A=∠C,
在△ADF和△CBE中,
|
∴△ADF≌△CBE(AAS);
故C可以证明;
D、(1)AD=CB;(3)∠B=∠D;(4)AD∥BC.
∵AD∥BC,
∴∠A=∠C,
在△ADF和△CBE中,
|
∴△ADF≌△CBE(ASA);
故D可以证明;
故选A.
点评:本题主要考查全等三角形的判定,掌握全等三角形的判定方法,即SSS、SAS、ASA、AAS和HL是解题的关键.

练习册系列答案
相关题目
毕节某商场的某纪念品原价150元,连续两次降价后售价为120元,降价率为x,则下列所列方程正确的是( )
| A、150(1+x)2=120 |
| B、120(1+x)2=150 |
| C、120(1-x)2=150 |
| D、150(1-x)2=120 |
实数4的算术平方根是( )
A、
| ||
B、±
| ||
| C、2 | ||
| D、±2 |
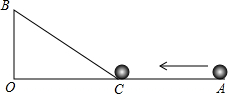 如图,∠AOB=90°,OA=49cm,OB=7cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
如图,∠AOB=90°,OA=49cm,OB=7cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?