题目内容
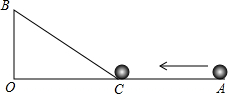如图，∠AOB=90°，OA=49cm，OB=7cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少？考点：勾股定理的应用
专题：
分析：首先得出小球滚动的速度与机器人行走的速度相等，运动时间相等，进而利用勾股定理求出即可．
解答：解：由题意得：小球滚动的速度与机器人行走的速度相等，运动时间相等，即BC=CA，
设AC为x，则OC=49-x，
由勾股定理可知OB2+OC2=BC2，
又∵OA=49，OB=7，
∴72+（49-x）2=x2，
解方程得出x=25（cm）．
答：如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是25cm．
设AC为x，则OC=49-x，
由勾股定理可知OB2+OC2=BC2，
又∵OA=49，OB=7，
∴72+（49-x）2=x2，
解方程得出x=25（cm）．
答：如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是25cm．
点评：此题主要考查了勾股定理的应用，根据题意得出BC=AC是解题关键．
练习册系列答案
相关题目
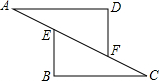如图所示，在△AFD和△BEC中，点A，E，F，C在同一直线上，有下列四个论断中选哪三个作为条件不能证明△ADF和△BCE全等（ ）（1）AD=CB；（2）AE=CF；（3）∠B=∠D；（4）AD∥BC．
| A、（1）（2）（3） |
| B、（1）（2）（4） |
| C、（2）（3）（4） |
| D、（1）（3）（4） |
温州市区某天的最高气温是10℃，最低气温是零下2℃，则该地这一天的温差是（ ）
| A、-12℃ | B、12℃ |
| C、8℃ | D、-8℃ |
已知实数a，b分别满足a2-4a+6=0，b2-4b+6=0，且a≠b，则
+
的值（ ）
| 1 |
| b |
| 1 |
| a |
| A、1.5 | ||
| B、-1.5 | ||
C、
| ||
D、-
|