题目内容
19.已知直角三角形ABC的两直角边长分别为6和8,则以第三边为边的正方形的面积为100.分析 由勾股定理求出直角三角形的斜边长,即第三边长,再由正方形的面积公式即可得出结果.
解答 解:由勾股定理得:斜边长=$\sqrt{{6}^{2}+{8}^{2}}$=10,
故以第三边为边的正方形的面积=102=100.
故答案为:100.
点评 本题考查了勾股定理、正方形面积的计算方法;熟练掌握勾股定理,由勾股定理求出斜边长是解决问题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
9.已知a,b互为倒数,|c-1|=2,则abc的值为( )
| A. | -1或3 | B. | -1 | C. | 3 | D. | ±2 |
10.下列方程中没有实数根的是( )
| A. | x2-x-1=0 | B. | x2+3x+2=0 | C. | 2015x2+11x-20=0 | D. | x2+x+2=0 |
7.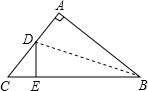 如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则tan∠DBE的值为( )
如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则tan∠DBE的值为( )
 如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则tan∠DBE的值为( )
如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则tan∠DBE的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{3\sqrt{73}}{73}$ | D. | $\frac{\sqrt{10}}{10}$ |
8.如果x是最大的负整数,y是绝对值最小的整数,则-x2015+y的值是( )
| A. | 2015 | B. | -1 | C. | 1 | D. | -2015 |
 如图,是长清园博园内的一个矩形花园,花园长为80米,宽为30米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为1400米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?
如图,是长清园博园内的一个矩形花园,花园长为80米,宽为30米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为1400米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?