题目内容
2.一次函数y=2x+b的图象与坐标轴围成的三角形面积为1,则b的值为( )| A. | 2 | B. | -2或$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2或-2 |
分析 分别令y=0和x=0可求得直线与坐标轴的交点,再利用三角形的面积可得到b的方程,可求得答案.
解答 解:
不妨设直线与x轴交于点A、与y轴交于点B,
在y=2x+b中,令y=0可得x=-$\frac{b}{2}$,令x=0可得y=b,
∴A(-$\frac{b}{2}$,0),B(0,b),
∴OA=|-$\frac{b}{2}$|,OB=|b|,
∵S△AOB=1,
∴$\frac{1}{2}$OA•OB=1,即$\frac{1}{2}$|-$\frac{b}{2}$||b|=1,
整理可得|b|2=4,
∴b=2或b=-2,
故选D.
点评 本题主要考查一次函数图象上点的坐标特征,用b分别表示出直线与两坐标轴的交点是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
13.用科学记数法得到的数字9.1×103精确到( )
| A. | 十分位 | B. | 千位 | C. | 十位 | D. | 百位 |
10.已知a-2b=3,则8-a+2b的值是( )
| A. | 3 | B. | 5 | C. | -3 | D. | -5 |
14.如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,CM:OC=2:5,则AB的长为( )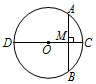

| A. | $\sqrt{91}cm$ | B. | 6cm | C. | 8cm | D. | 4cm |
12.下列说法正确的是( )
| A. | 9的算术平方根是3 | B. | 4的平方根是2 | ||
| C. | -3的平方根是$\sqrt{-3}$ | D. | 8的立方根是±2 |