题目内容
14.如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,CM:OC=2:5,则AB的长为( )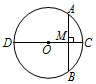
| A. | $\sqrt{91}cm$ | B. | 6cm | C. | 8cm | D. | 4cm |
分析 由圆的直径求出半径,得出OC的长,根据CM与OC的比值求出CM、OM的长,连接OA,由DC垂直于AB,利用垂径定理得到M为AB的中点,在直角三角形AOM中,由OA与OM的长,利用勾股定理求出AM的长,即可求出AB的长.
解答 解:连接OA,
∵直径CD=10cm,
∴OA=OC=$\frac{1}{2}$OD=5cm,
∵CM:OC=2:5,
∴CM=2cm,
∴OM=3cm,
∵AB⊥CD,
∴AB=2AM=2$\sqrt{O{A}^{2}-O{M}^{2}}$=8cm,
故选:C.
点评 此题考查了垂径定理,以及勾股定理,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在2,0,-1.5,-1这四个数中,绝对值最小的数是( )
| A. | 2 | B. | 0 | C. | -1.5 | D. | -1 |
2.一次函数y=2x+b的图象与坐标轴围成的三角形面积为1,则b的值为( )
| A. | 2 | B. | -2或$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2或-2 |
19. 将如图折叠成正方体后,与“七”字相对面上的汉字是( )
将如图折叠成正方体后,与“七”字相对面上的汉字是( )
 将如图折叠成正方体后,与“七”字相对面上的汉字是( )
将如图折叠成正方体后,与“七”字相对面上的汉字是( )| A. | 育 | B. | 才 | C. | 学 | D. | 校 |
3.计算4-2的结果是( )
| A. | -16 | B. | -$\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | -$\frac{1}{16}$ |
4.已知下列函数:①y=-$\frac{2}{x}$+3②y=3(3-x)③y=3x-x2④y=-$\frac{x}{3}$⑤y=5,其中是一次函数的是( )
| A. | ①②③④⑤ | B. | ②④ | C. | ①③⑤ | D. | ②④⑤ |