题目内容
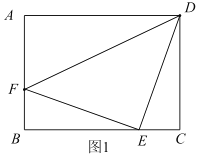
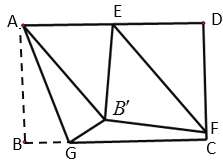
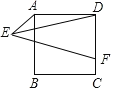
【题目】如图，正方形ABCD的边长AB=8，E为平面内一动点，且AE=4，F为CD上一点，CF=2，连接EF，ED，则EF
ED的最小值为( )
A.6
B.4C.4D.6
【答案】A
【解析】
如图（见解析），在AD边上取点H，使得
，连接EH、FH，先根据正方形的性质得出
，
，再根据相似三角形的判定与性质得出
，从而可得
，然后利用三角形的三边关系定理、两点之间线段最短可得
取得最小值时，点E的位置，最后利用勾股定理求解即可得．
如图，在AD边上取点H，使得，连接EH、FH
四边形ABCD是正方形
，
，
，即
又
，即
由三角形的三边关系定理得：
由题意得：点E的轨迹是在以点A为圆心，AE长为半径的圆上
由两点之间线段最短可知，当点E位于FH与圆A的交点
时，
取得最小值，最小值为
，
在
中，由勾股定理得
即的最小值为
故选：A．
练习册系列答案
相关题目
【题目】二次函数
（
是常数，
）的自变量
与函数值
的部分对应值如下表：
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当
时，与其对应的函数值
．有下列结论：①
；②
和3是关于的方程
的两个根；③
．其中，正确结论的个数是（ ）
A. 0B. 1C. 2D. 3
