题目内容

3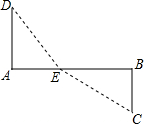．如图铁路上A，B两点相距40千米，C，D为两村庄，DA⊥AB，CB⊥AB，垂足分别为A和B，DA=24千米，CB=16千米．现在要在铁路旁修建一个煤栈E，使得C，D两村到煤栈的距离相等，那么煤栈E应距A点（　　）
A．20千米B．16千米C．12千米D．无法确定

分析 根据题意利用勾股定理得出AD2+AE2=BE2+BC2，进而求出即可．

解答 解：设AE=xkm，则BE=（40-x）km，
∵DA⊥AB，CB⊥AB，C，D两村到煤栈的距离相等，
∴AD2+AE2=BE2+BC2，
故242+x2=（40-x）2+162，
解得：x=16，
则煤栈E应距A点16km．
故选：B．

点评 此题主要考查了勾股定理的应用，根据题意DE=EC，进而利用勾股定理得出是解题关键．

练习册系列答案
相关题目
13．（1）计算：2-1+$\sqrt{（-2）^{2}}$-（$\root{3}{1949}$-$\sqrt{2009}$）0-$\root{3}{-\frac{1}{8}}$
（2）解不等式：-1≤$\frac{3-2x}{3}$≤5．
14．下列二次根式中，与$\sqrt{ab}（{a＞0，b＞0}）$是同类二次根式的是（　　）
A．$\sqrt{\frac{b}{a}}$B．$\sqrt{\frac{{{a^2}{b^2}}}{4}}$C．$\sqrt{{a^2}{b^3}}$D．$\sqrt{\frac{2}{ab}}$
11．从哈尔滨开往某市的特快列车，途中要停靠两个站点，如果任意两站间的票价都不同，那么不同的票价有（　　）
A．3种B．4种C．6种D．12种
18．计算
（1）24+（-14）+（-16）+8：
（2）1-$\frac{4}{7}$+$\frac{1}{5}$-$\frac{3}{7}$+$\frac{9}{5}$；
（3）-54×2$\frac{1}{4}$÷（-4$\frac{1}{2}$）×$\frac{2}{9}$              
（4）（$\frac{1}{2}$-$\frac{5}{9}$+$\frac{7}{12}$）×（-36）
（5）-22×7-（-3）×6+5                
（6）-14-[1-（1-0.5×$\frac{1}{3}$）]×6．
8．如果最简二次根式2$\sqrt{x+4}$和$\sqrt{2x+1}$是同类二次根式，那么x=3．
15．下列各命题中，真命题的是 （　　）
A．每个命题都有逆命题B．每个定理都有逆定理
C．真命题的逆命题一定是真命题D．假命题的逆命题一定是假命题
12．如图，将矩形纸片ABCD折叠，使AB边与对角线AC重合，点B落在点F处，折痕为AE．若AD=8，EF=3，则AE的长为$3\sqrt{5}$．
13．不等式2x-3≤1的解集是（　　）
A．x≤1B．x≤2C．x≥1D．x≥2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网