题目内容
13.(1)计算:2-1+$\sqrt{(-2)^{2}}$-($\root{3}{1949}$-$\sqrt{2009}$)0-$\root{3}{-\frac{1}{8}}$(2)解不等式:-1≤$\frac{3-2x}{3}$≤5.
分析 (1)原式第一项利用负整数指数幂法则计算,第二项利用二次根式性质化简,第三项利用零指数幂法则,最后一项利用立方根定义计算即可得到结果;
(2)已知双向不等式变形,化为不等式组,求出解集即可.
解答 解:(1)原式=$\frac{1}{2}$+2-1+$\frac{1}{2}$=2;
(2)方程整理得:$\left\{\begin{array}{l}{\frac{3-2x}{3}≥-1①}\\{\frac{3-2x}{3}≤5②}\end{array}\right.$,
由①得:x≤3,
由②得:x≥-6,
则方程组的解为-6≤x≤3.
点评 此题考查了实数的运算,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
3.已知O为平行四边形ABCD对角线的交点,△AOB的面积为1,则平行四边形的面积为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.下列运算中,正确的是( )
| A. | a•a2=a2 | B. | (-a2)2=a4 | C. | a3•a3=2a3 | D. | (a2b)3=a2•b3 |
8.若x、y分别变为原来的3倍,则分式$\frac{3xy}{x-y}$(xy≠0)的值( )
| A. | 不变 | B. | 是原来的3倍 | C. | 是原来的9倍 | D. | 以上说法都不对 |
18.若$\sqrt{3m-1}$有意义,则m能取的最小整数值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
2.下列方程中,有实数根的是( )
| A. | $\sqrt{{x^2}+1}$=0 | B. | $\sqrt{1-x}$+$\frac{1}{3}$=0 | C. | $\sqrt{x+1}$=2 | D. | $\sqrt{x-1}$+$\sqrt{1-x}$=2 |
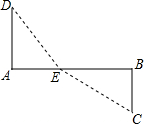 如图铁路上A,B两点相距40千米,C,D为两村庄,DA⊥AB,CB⊥AB,垂足分别为A和B,DA=24千米,CB=16千米.现在要在铁路旁修建一个煤栈E,使得C,D两村到煤栈的距离相等,那么煤栈E应距A点( )
如图铁路上A,B两点相距40千米,C,D为两村庄,DA⊥AB,CB⊥AB,垂足分别为A和B,DA=24千米,CB=16千米.现在要在铁路旁修建一个煤栈E,使得C,D两村到煤栈的距离相等,那么煤栈E应距A点( )