题目内容
14.下列二次根式中,与$\sqrt{ab}({a>0,b>0})$是同类二次根式的是( )| A. | $\sqrt{\frac{b}{a}}$ | B. | $\sqrt{\frac{{{a^2}{b^2}}}{4}}$ | C. | $\sqrt{{a^2}{b^3}}$ | D. | $\sqrt{\frac{2}{ab}}$ |
分析 先将各选项化简,再根据同类二次根式的定义解答.
解答 解:A、$\sqrt{\frac{b}{a}}=\frac{\sqrt{ab}}{a}$与$\sqrt{ab}$被开方数相同,故是同类二次根式;
B、$\sqrt{\frac{{a}^{2}{b}^{2}}{4}}=\frac{ab}{2}$与$\sqrt{ab}$被开方数不相同,故不是同类二次根式;
C、$\sqrt{{a}^{2}{b}^{3}}=ab\sqrt{b}$与$\sqrt{ab}$被开方数不相同,故不是同类二次根式;
D、$\sqrt{\frac{2}{ab}}=\frac{\sqrt{2ab}}{ab}$与$\sqrt{ab}$被开方数不相同,故不是同类二次根式;
故选A.
点评 此题考查同类二次根式的定义,正确对根式进行化简,以及正确理解同类二次根式的定义是解决问题的关键.

练习册系列答案
相关题目
4.下列运算中,正确的是( )
| A. | a•a2=a2 | B. | (-a2)2=a4 | C. | a3•a3=2a3 | D. | (a2b)3=a2•b3 |
2.下列方程中,有实数根的是( )
| A. | $\sqrt{{x^2}+1}$=0 | B. | $\sqrt{1-x}$+$\frac{1}{3}$=0 | C. | $\sqrt{x+1}$=2 | D. | $\sqrt{x-1}$+$\sqrt{1-x}$=2 |
3.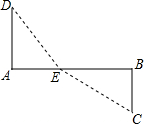 如图铁路上A,B两点相距40千米,C,D为两村庄,DA⊥AB,CB⊥AB,垂足分别为A和B,DA=24千米,CB=16千米.现在要在铁路旁修建一个煤栈E,使得C,D两村到煤栈的距离相等,那么煤栈E应距A点( )
如图铁路上A,B两点相距40千米,C,D为两村庄,DA⊥AB,CB⊥AB,垂足分别为A和B,DA=24千米,CB=16千米.现在要在铁路旁修建一个煤栈E,使得C,D两村到煤栈的距离相等,那么煤栈E应距A点( )
 如图铁路上A,B两点相距40千米,C,D为两村庄,DA⊥AB,CB⊥AB,垂足分别为A和B,DA=24千米,CB=16千米.现在要在铁路旁修建一个煤栈E,使得C,D两村到煤栈的距离相等,那么煤栈E应距A点( )
如图铁路上A,B两点相距40千米,C,D为两村庄,DA⊥AB,CB⊥AB,垂足分别为A和B,DA=24千米,CB=16千米.现在要在铁路旁修建一个煤栈E,使得C,D两村到煤栈的距离相等,那么煤栈E应距A点( )| A. | 20千米 | B. | 16千米 | C. | 12千米 | D. | 无法确定 |
4.在全国特殊困难地区,中央财政每年将投入专款实施营养改善计划,每名学生每天补贴3元,惠及近2600万名农村学生.将2600万用科学记数法表示为( )
| A. | 2.6×106 | B. | 2.6×107 | C. | 0.26×108 | D. | 26×106 |