题目内容
这是某单位的平面示意图,已知大门的坐标为(﹣3,0),花坛的坐标为(0,﹣1).
(1)根据上述条件建立平面直角坐标系;
建筑物 A 的坐标为(3,1),请在图中标出 A 点的位置.
(3)建筑物 B 在大门北偏东 45°的方向,并且 B 在花坛的正北方向处,请直接写出 B 点的坐标.
(4)在 y 轴上找一点 C,使△ABC 是以 AB 腰的等腰三角形,请直接写出点 C 的坐标.
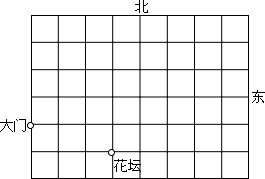
【考点】等腰三角形的判定;坐标确定位置;方向角.
【分析】(1)以花坛向上 1 个单位为坐标原点,建立平面直角坐标系即可; 根据平面直角坐标系标出点 A 的位置即可;
(3)根据方向角确定点 B 的位置即可;
(4)设 C(0,y),利用等腰三角形的性质和两点间的距离公式进行解答.
【解答】解:(1)如图所示; 点 A 如图所示;
(3)点 B 如图所示:点 B(0,3);
(4)设 C(0,y).
∵A(3,1),B(0,3),
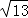 ∴AB=
∴AB= 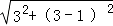 = .
= .
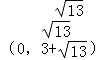 ①当 AB=BC 时,|3﹣y|= , 解得 y=3+
①当 AB=BC 时,|3﹣y|= , 解得 y=3+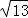 或 y=3﹣ ,
或 y=3﹣ ,
则点 C 的坐标是 或 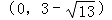 ;
;
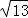 ②当 AB=AC 时,
②当 AB=AC 时,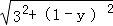 = , 解得 y=﹣1 或 y=3.
= , 解得 y=﹣1 或 y=3.
则点 C 的坐标是(0,﹣1)或(0,3)(舍去)
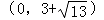
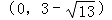 综上所述,点 C 的坐标是: , 或(0,﹣1).
综上所述,点 C 的坐标是: , 或(0,﹣1).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
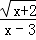 中自变量 x 的取值范围是
中自变量 x 的取值范围是  如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ), 点 C 的坐标为(1,0),点 P 为斜边 OB 上的一动点,则△PAC 周长的最小值为 .
如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ), 点 C 的坐标为(1,0),点 P 为斜边 OB 上的一动点,则△PAC 周长的最小值为 .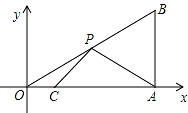
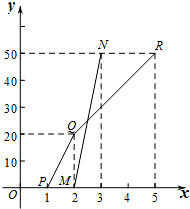
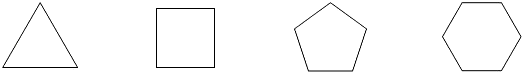
 根据上表,猜想正 n 边形有 n 条对称轴.
根据上表,猜想正 n 边形有 n 条对称轴.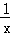 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )