题目内容
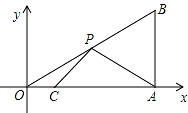
 如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ), 点 C 的坐标为(1,0),点 P 为斜边 OB 上的一动点,则△PAC 周长的最小值为 .
如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ), 点 C 的坐标为(1,0),点 P 为斜边 OB 上的一动点,则△PAC 周长的最小值为 .
 +2【考点】轴对称-最短路线问题;坐标与图形性质.
+2【考点】轴对称-最短路线问题;坐标与图形性质.
【分析】作 A 关于 OB 的对称点 D,连接 CD 交 OB 于 P,连接 AP,过 D 作 DN⊥OA 于 N,则此 时 PA+PC 的值最小,求出 AM,求出 AD,求出 DN、CN,根据勾股定理求出 CD,即可得出答案.
【解答】解:作 A 关于 OB 的对称点 D,连接 CD 交 OB 于 P,连接 AP,过 D 作 DN⊥OA 于 N, 则此时 PA+PC 的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
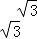 ∵B(3, ),
∵B(3, ),
∴AB= ,OA=3,∠B=60°,由勾股定理得:OB=2 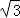 , 由三角形面积公式得:
, 由三角形面积公式得: 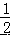 ×OA×AB=
×OA×AB= 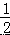 ×OB×AM,
×OB×AM,
∴AM= 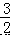 ,
,
∴AD=2× 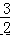 =3,
=3,
∵∠AMB=90°,∠B=60°,
∴∠BAM=30°,
∵∠BAO=90°,
∴∠OAM=60°,
∵DN⊥OA,
∴∠NDA=30°,
∴AN= 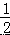 AD=
AD= 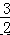 ,由勾股定理得:DN=
,由勾股定理得:DN= 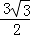 ,
,
∵C(1,0),
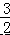
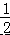 ∴CN=AC﹣AN=2﹣ = ,
∴CN=AC﹣AN=2﹣ = ,

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
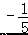
 A. B.﹣5 C. D.5
A. B.﹣5 C. D.5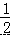
 ﹣(﹣1)2﹣( ﹣1)0+
﹣(﹣1)2﹣( ﹣1)0+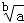 的值为
的值为 
 B.
B.  C.
C.  D.
D.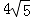 ,△BCE 的面积= .
,△BCE 的面积= .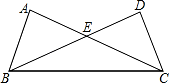
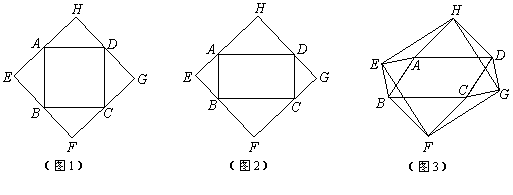
 的边
的边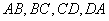 为斜边分别向外侧作等腰直角三角形,直角顶点分别为
为斜边分别向外侧作等腰直角三角形,直角顶点分别为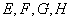 ,顺次连结这四个点,得四边形
,顺次连结这四个点,得四边形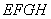 .如图1,当四边形
.如图1,当四边形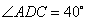 ,
,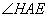 的度数;
的度数;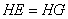 ;
;