题目内容
3．不画出图象，回答下列问题．（1）函数y=-2（x-3）2+2的图象可以看成是由函数y=-2x2的图象通过怎样平移得到的？
（2）说出函数y=-2（x-3）2+2的图象的开口方向、对称轴和顶点坐标；
（3）如果要将函数y=-2（x-3）2+2的图象经过适当的平移．得到函数y=-2（x+1）2-1的图象．那么应该怎样平移？
分析 （1）根据函数图象的平移规律，可得答案．
（2）根据抛物线解析式直接回答问题．
（3）根据抛物线顶点的平移变换规律来推知抛物线的平移变换规律．
解答 解：（1）抛物线y=-2x2的顶点坐标是（0，0），抛物线y=-2（x-3）2+2的顶点坐标是（3，2），
∵顶点（0，0）向上平移3个单位，向右平移2个单位得到（3，2），
∴函数y=-2（x-3）2+2的图象可以看成是由函数y=-2x2的图象向上平移3个单位，向右平移2个单位得到的；
（2）函数y=-2（x-3）2+2的图象的开口方向向下，对称轴是x=3，其顶点坐标是（3，2）；
（3）抛物线y=-2（x-3）2+2的顶点坐标是（3，2），抛物线y=-2（x+1）2-1的顶点坐标是（-1，-1），
∵顶点（3，2）向下平移4个单位，向左平移3个单位得到（-1，-1），
∴函数y=-2（x+1）2-1的图象可以看成是由函数y=-2（x-3）2+2的图象向下平移4个单位，向左平移3个单位得到的．
点评 本题考查了二次函数图象与几何变换，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．
练习册系列答案
相关题目
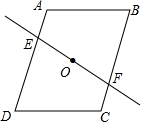如图，直线EF经过平行四边形ABCD的对角线的交点，若AE=3cm，四边形AEFB的面积为15cm2，则CF=3cm，四边形EDCF的面积为15cm2．
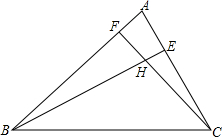在△ABC中，已知∠ABC=45°，∠ACB=60°，BE是AC上的高，CF交AB于点F，交BE于点H，且∠BHC=105°，△BFH是直角三角形吗？为什么？
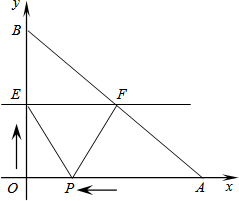如图，已知A、B两点的坐标分别为（40，0），（0，30），动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动，动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动（即EF∥x轴），并且分别与y轴、线段AB交于点E、F，连接EP、FP，设动点P与动直线EF同时出发，运动时间为t秒．
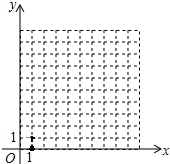如图，在平面直角坐标系中，一只蜘蛛P从点A（1，0），选择以下规定动作爬行