题目内容
2.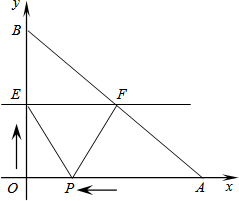 如图,已知A、B两点的坐标分别为(40,0),(0,30),动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动,动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.
如图,已知A、B两点的坐标分别为(40,0),(0,30),动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动,动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.(1)求t=15时,△PEF的面积;
(2)当t为何值时,△EOP与△BOA相似.
分析 (1)先根据A、B两点的坐标分别为(40,0),(0,30)得出OA及OB的长,再由EF∥x轴得出EF是△BOA的中位线,再根据三角形的面积公式即可得出结论;
(2)用t表示出OE及OP的长,再分△EOP∽△BOA与△EOP∽△AOB两种情况进行讨论.
解答 解:(1)∵A、B两点的坐标分别为(40,0),(0,30),
∴OA=40,OB=30.
∵动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动(即EF∥x轴),
∴t=15时,BE=30-15=15,
∵EF∥x轴,
∴EF是△BOA的中位线,
∴EF=$\frac{1}{2}$OA=20,
∴S△PEF=$\frac{1}{2}$EF•OE=$\frac{1}{2}$×20×15=150;
(2)∵动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动,动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动(即EF∥x轴),
∴OE=t,OP=40-2t,
∴当△EOP∽△BOA时,$\frac{OE}{OB}$=$\frac{OP}{OA}$,即$\frac{t}{30}$=$\frac{40-2t}{40}$,解得t=12(秒);
当△EOP∽△AOB时,$\frac{OP}{OB}$=$\frac{OE}{OA}$,即$\frac{40-2t}{30}$=$\frac{t}{40}$.解得t=$\frac{160}{11}$(秒).
综上所述,当t=12秒或t=$\frac{160}{11}$秒时,△EOP与△BOA相似.
点评 本题考查的是相似形综合题,涉及到三角形中位线定理、三角形的面积公式及相似三角形的判定与性质等知识,在解答(2)时要注意进行分类讨论.

练习册系列答案
相关题目
18.如果把分式$\frac{x+2y}{x+y}$中的x、y的值都变为原来的10倍,那么分式的值( )
| A. | 变成原来的10倍 | B. | 缩小为原来的10倍 | ||
| C. | 是原来的$\frac{2}{3}$ | D. | 不变 |
11.已知a>b,则下列不等式中成立的是( )
| A. | -a>-b | B. | 4a<4b | C. | 2a-1>3b-1 | D. | a+3>b+3 |
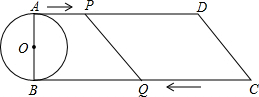 如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s速度运动.P、Q分别从点A、C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t s,问:
如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s速度运动.P、Q分别从点A、C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t s,问: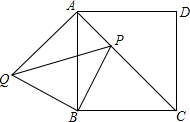 如图,在正方形ABCD中,点P是对角线AC上一点,把△BPC绕着点B逆时针旋转得到△BQA.
如图,在正方形ABCD中,点P是对角线AC上一点,把△BPC绕着点B逆时针旋转得到△BQA.