题目内容
12.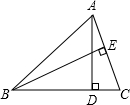 如图,在△ABC中,AC=2cm,BC=3cm,△ABC的高AD与BE的比是$\frac{2}{3}$.
如图,在△ABC中,AC=2cm,BC=3cm,△ABC的高AD与BE的比是$\frac{2}{3}$.
分析 根据三角形的面积公式得出$\frac{1}{2}$BC•AD=$\frac{1}{2}$AC•BE,再把AC和BC的值代入即可得出△ABC的高AD与BE的比.
解答 解:∵S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$AC•BE,AC=2cm,BC=3cm,
∴$\frac{1}{2}$×3•AD=$\frac{1}{2}$×2•BE,
∴$\frac{3}{2}$AD=BE,
∴$\frac{AD}{BE}$=$\frac{2}{3}$;
故答案为:$\frac{2}{3}$.
点评 此题考查了比例线段和三角形的面积,利用两个底边和对应的高线列出面积的表达式是解题的关键.

练习册系列答案
相关题目
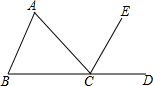 如图,点B、C、D在同一直线上,∠A=∠B.
如图,点B、C、D在同一直线上,∠A=∠B.