题目内容
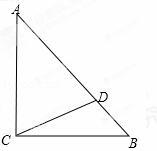
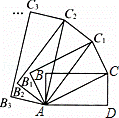
如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形ABnCnCn﹣1的面积为 .
 : 解:
: 解:
∵四边形ABCD是矩形,
∴AD⊥DC,
∴AC= =
= =
= ,
,
∵按逆时针方向作矩形ABCD的相似矩形AB1C1C,
∴矩形AB1C1C的边长和矩形ABCD的边长的比为 :2
:2
∴矩形AB1C1C的面积和矩形ABCD的面积的比5:4,
∵矩形ABCD的面积=2×1=2,
∴矩形AB1C1C的面积= ,
,
依此类推,矩形AB2C2C1的面积和矩形AB1C1C的面积的比5:4
∴矩形AB2C2C1的面积=
∴矩形AB3C3C2的面积= ,
,
按此规律第n个矩形的面积为:
故答案为: .
.
点评: 本题考查了矩形的性质,勾股定理,相似多边形的性质,解此题的关键是能根据求出的结果得出规律.

练习册系列答案
相关题目
 )的抛物线y=
)的抛物线y=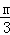 (x+1)(x﹣3)(m为常数,且m>0)与x轴交于点A、B(点A位于B的左侧),与y轴交于点C.
(x+1)(x﹣3)(m为常数,且m>0)与x轴交于点A、B(点A位于B的左侧),与y轴交于点C.

 ,电视正在播放新闻联播
,电视正在播放新闻联播
 的三视图如图所示,这个几何体是( )
的三视图如图所示,这个几何体是( )
 ∠A的平分线交CD于E;
∠A的平分线交CD于E;