题目内容
如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.
 (1)求证:AB与⊙O相切;
(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是4,求线段BF的长?
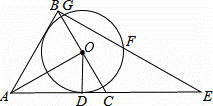
解:(1)过点O作OM⊥AB,垂足是M.
∵⊙O与AC相切于点D.
∴OD⊥AC,
∴∠ADO=∠AMO=90°.
∵△ABC是等边三角形,
∴∠DAO=∠NAO,
∴OM=OD.
∴AB与⊙O相切;
(2)过点O作ON⊥BE,垂足是N,连接OF.
∵O是BC的中点,
∴OB=2.
在直角△OBM中,∠MBO=60du6,
∴OM=OB•sin60°= ,BM=OB•cos60°=1.
,BM=OB•cos60°=1.
∵BE⊥AB,
∴四边形OMBN是矩形.
∴ON=BM=1,BN=OM= .
.
∵OF=OM= ,
,
由勾股定理得NF= .
.
∴BF=BN+NF= +
+ .
.


练习册系列答案
相关题目
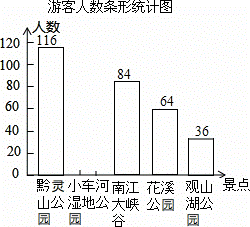
近年来,随着创建“生态文明城市”活动的开展,我市的社会知名度越来越高,吸引了很多外地游客,某旅行社对5月份本社接待外地游客来我市各景点旅游的人数作了一次抽样调查,并将调查结果绘制成如下两幅不完整的统计图表:
游客人数统计表
| 景点 | 频数(人数) | 频率 |
| 黔灵山公园 | 116 | 0.29 |
| 小车河湿地公园 | 0.25 | |
| 南江大峡谷 | 84 | 0.21 |
| 花溪公园 | 64 | 0.16 |
| 观山湖公园 | 36 | 0.09 |
(1)此次共调查 人,并补全条形统计图;
(2)由上表提供的数据可以制成扇形统计图,求“南江大峡谷”所对的圆心角的度数;
(3)该旅行社预计7月份接待来我市的游客有2500人,根据以上信息,请你估计去黔灵山公园的游客大约有多少人?
 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( ) B.
B.
 D.
D.
 我市质检部分对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.
我市质检部分对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.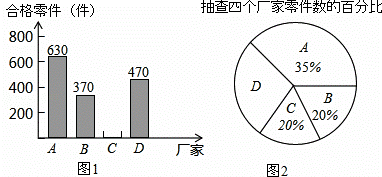
 有意义,则实数x的取值范围是
有意义,则实数x的取值范围是 


 D.24°
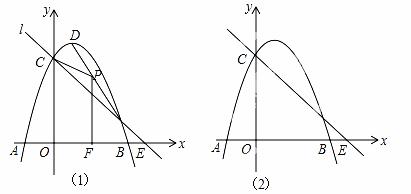
D.24°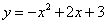 与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).