题目内容
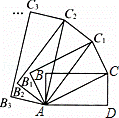
如图，菱形ABCD的边长为2，∠DAB=60°，E为BC的中点，在对角线AC上存在一点P，使△PBE的周长最小，则△PBE的周长的最小值为 ．
3： 解：连接BD，与AC的交点即为使△PBE的周长最小的点P；如图所示：
∵四边形ABCD是菱形，
∴AC⊥BD，AB=BC=CD=DA=2，
∴∠BPC=90°，
∵E为BC的中点，
∴BE=
BC=1，PE=BC=1，
∴PE=BE，
∵∠DAB=60°，
∴∠ABC=120°，
∴∠PBE=60°，
∴△PBE是等边三角形，
∴PB=BE=PE=1，
∴PB+BE+PE=3；
故答案
为：3．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
B．
C．
D． 
我市质检部分对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测，通过检测得出C厂家的合格率为95%，并根据检测数据绘制了如图1、图2两幅不完整的统计图．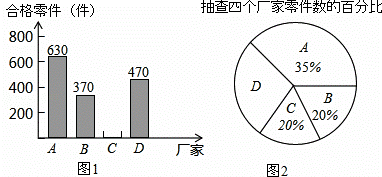
的绝对值是（ ）
C． 2 D． ﹣2
