Question

1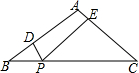．在△ABC中，AB=AC=5，BC=8，点P是BC上的动点，过点P作PD⊥AB于点D，PE⊥AC于E，则PD+PE=$\frac{24}{5}$．

Answer 1

分析 作AF⊥BC于F，根据等腰三角形三线合一的性质得出BF=CF=$\frac{1}{2}$BC=4，然后根据勾股定理求得AF=3，连接AP，由图可得：S_ABC=S_ABP+S_ACP，代入数值，解答出即可．

解答 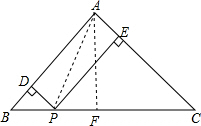解：作AF⊥BC于F，
∵AB=AC，
∴BF=CF=$\frac{1}{2}$BC=4，
∴AF=$\sqrt{{5}^{2}-{4}^{2}}$=3．
连接AP，
由图可得，S_ABC=S_ABP+S_ACP，
∵PD⊥AB于D，PE⊥AC于E，AB=AC=5，
∵S_△APB+S_△APC=S_△ABC，
∴$\frac{1}{2}$×5×PD+$\frac{1}{2}$×5×PE=$\frac{1}{2}$×8×3，
∴PD+PE=$\frac{24}{5}$．
故答案为$\frac{24}{5}$．

点评 本题主要考查了等腰三角形的性质，解答时注意，将一个三角形的面积转化成两个三角形的面积和；体现了转化思想．