题目内容
9.分解因式:1+x+x(1+x)+x(1+x)2+x(1+x)3.看看有什么规律,利用你发现的规律直接写出多项式1+x+x(1+x)+x(1+x)2+…+x(1+x)n分解因式的结果.分析 直接利用提取公因式法分解因式,进而得出规律求出答案即可.
解答 解:∵1+x+x(1+x)+x(1+x)2+x(1+x)3
=(1+x)+x(1+x)+x(1+x)2+x(1+x)3
=(1+x)[1+x+x(1+x)+x(1+x)2]
=(1+x)(1+x)[1+x+x(1+x)]
=(1+x)2(1+x)(1+x)
=(1+x)4,
∴由以上可得:
1+x+x(1+x)+x(1+x)2+…+x(1+x)n
=(1+x)n+1.
点评 此题主要考查了提取公因式法分解因式,正确根据已知多项式分解因式得出规律是解题关键.

练习册系列答案
相关题目
20.将抛物线y=x2沿y轴向下平移2个单位,得到的抛物线的解析式为( )
| A. | y=x2+2 | B. | y=x2-2 | C. | y=(x+2)2 | D. | y=(x-2)2 |
 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于点D,且AB=12,BD=15,则点D到BC的距离为9.
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于点D,且AB=12,BD=15,则点D到BC的距离为9.
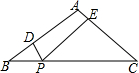 在△ABC中,AB=AC=5,BC=8,点P是BC上的动点,过点P作PD⊥AB于点D,PE⊥AC于E,则PD+PE=$\frac{24}{5}$.
在△ABC中,AB=AC=5,BC=8,点P是BC上的动点,过点P作PD⊥AB于点D,PE⊥AC于E,则PD+PE=$\frac{24}{5}$.