题目内容
10.已知x1,x2是方程x2+3x-$\sqrt{5}$=0的两根,求x12-x22+4x1-2x2的值.分析 利用一元二次方程根与系数的关系,求出方程的两根之和和两根之积,再将代数式加以整理得:x12-x22+4x1-2x2=x12+3x1-(x22+3x2)+(x1+x2),再代入数值求得答案即可.
解答 解:∵x1,x2是方程x2+3x-$\sqrt{5}$=0的两根,
∴x12+3x1=$\sqrt{5}$,x22+3x2=$\sqrt{5}$,x1+x2=-3,
∴x12-x22+4x1-2x2
=x12+3x1-(x22+3x2)+(x1+x2)
=$\sqrt{5}$-$\sqrt{5}$-3
=-3.
点评 本题考查一元二次方程根与系数的关系和一元二次方程解的意义,遇到此类求代数式求值问题,应对代数式进行适当的变形,使其含有两根和、两根积的形式,再求得其值.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
20.将抛物线y=x2沿y轴向下平移2个单位,得到的抛物线的解析式为( )
| A. | y=x2+2 | B. | y=x2-2 | C. | y=(x+2)2 | D. | y=(x-2)2 |
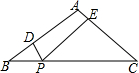 在△ABC中,AB=AC=5,BC=8,点P是BC上的动点,过点P作PD⊥AB于点D,PE⊥AC于E,则PD+PE=$\frac{24}{5}$.
在△ABC中,AB=AC=5,BC=8,点P是BC上的动点,过点P作PD⊥AB于点D,PE⊥AC于E,则PD+PE=$\frac{24}{5}$.