题目内容
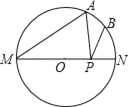
【题目】如图,MN是⊙O的直径,MN=2a,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则 PA+PB的最小值为_____.(用含a的代数式表示)
【答案】![]() a
a
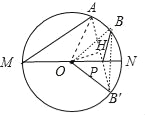
【解析】作B点关于MN的对称点B′,连接AB′交MN于P,如图,
则PB=PB′,
∴PA+PB=PA+PB′=AB′,
∴此时PA+PB的值最小,
∵∠AMN=40°,
∴∠AON=80°,
∵点B为弧AN的中点,
∴∠BON=![]() ∠AON=40°,
∠AON=40°,
∵B点关于MN的对称点B′,
∴∠B′ON=40°,
∴∠AOB′=120°,
作OH⊥AB′于H,如图,则AH=B′H,
在Rt△AOH中,∠A=30°,
∴OH=![]() OA=
OA=![]() a,
a,
∴AH=![]() OH=
OH=![]() a,
a,
∴AB′=2AH=![]() a,
a,
即 PA+PB的最小值为![]() a.
a.
故答案为: ![]() a.
a.

练习册系列答案
相关题目