题目内容
【题目】已知:![]() ,
,![]() 平分
平分![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() 、
、![]() 分别是射线
分别是射线![]() 、
、![]() 上的动点(
上的动点(![]() 、
、![]() 不与点
不与点![]() 重合),连接
重合),连接![]() 交射线
交射线![]() 于点
于点![]() .设
.设![]() .
.

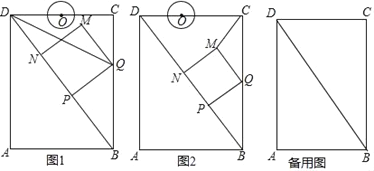
(1)如图1,若![]() ,则:①
,则:①![]() ______;②当
______;②当![]() 时,
时,![]() ______
______![]() .
.
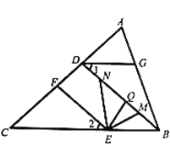
(2)如图2,若![]() ,垂足为
,垂足为![]() ,则是否存在这样的
,则是否存在这样的![]() 的值,使得
的值,使得![]() 中存在两个相等的角?若存在,求出
中存在两个相等的角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)①![]() ;②
;②![]() ;(2)存在这样的
;(2)存在这样的![]() 的值,使得
的值,使得![]() 中有两个相等的角,且
中有两个相等的角,且![]() 、
、![]() 、
、![]() 、
、![]() .
.
【解析】
(1)①利用平行线的性质可得∠ABO=∠BON,求出∠BON即可.
②求出∠MAB,∠BAD即可解决问题.
(2)分两种情形讨论求解即可.①如图2中,当点D在线段OB上时,②如图2-1中,当点D在OB的延长线上时.
解:(1)①∵∠MON=56°,OE平分∠MON,
∴∠AOB=∠BON=28°,
∵AB∥ON,
∴∠ABO=∠BON=28°.
②∵∠BAD=∠BDA,
∴∠BAD= ![]() (180°-28°)=76°,
(180°-28°)=76°,
∵AB∥ON,
∴∠MAB=∠MON=56°,
∴∠OAC=180°-∠MAB-∠BAD=180°-56°-76°=48°,
故答案为28°,48°.
(2)①如图2中,当点D在线段OB上时,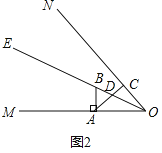
∵AB⊥OM,
∴∠OAB=90°,
∵∠AOB=28°,
∴∠ABO=62°,
当∠BAD=∠ABD=62°时,x=∠OAC=90°-62°=28°.
当∠BAD=∠BDA时,∠BAD=∠BDA=59°,x=90°-59°=31°.
当∠ADB=∠ABD=62°时,∠BAD=56°,x=90°-56°=34°.
②如图2-1中,当点D在OB的延长线上时,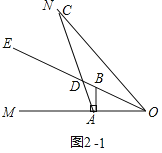
∵∠ABD=180°-62°=118°,
∴只有∠ADB=∠BAD,此时x=121°.
综上可知,存在这样的![]() 的值,使得
的值,使得![]() 中有两个相等的角,
中有两个相等的角,
且![]() 、
、![]() 、
、![]() 、
、![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目