题目内容
19.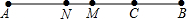 如图,线段AB=8cm,M为线段AB的中点,C为线段MB上一点,且MC=2cm,N为线段AC的中点,则线段MN的长为( )
如图,线段AB=8cm,M为线段AB的中点,C为线段MB上一点,且MC=2cm,N为线段AC的中点,则线段MN的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据中点的性质,可得MB,根据线段的和差,可得AC的长,根据线段的和差,可得AC的长,再根据线段中点的性质,可得答案.
解答 解:由线段AB=8cm,M为线段AB的中点,得
AM=BM=4cm.
由线段和差,得
CB=MB-MC=4-2=2cm.
AC=AB-BC=8-2=6cm.
由N为线段AC的中点,得
NC=$\frac{1}{2}$AC=3cm,
NM=NC-MC=3-2=1cm.
点评 本题考查了两点间的距离,利用线段的和差、线段中点的性质是解题关键.

练习册系列答案
相关题目
4.下列约分正确的是( )
| A. | $\frac{{x}^{6}}{{x}^{2}}$=x3 | B. | $\frac{x+y}{{x}^{2}+xy}$=$\frac{1}{x}$ | C. | $\frac{x+y}{x+y}$=0 | D. | $\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{1}{2}$ |
11.以下列各组线段为边,能组成三角形的是( )
| A. | 1cm,1cm,1cm | B. | 5cm,5cm,10cm | C. | 1cm,2cm,3cm | D. | 2cm,3cm,6cm |
8.在△ABC中,AB=AC,∠BAC=50°,则∠C的度数为( )
| A. | 75° | B. | 65° | C. | 55° | D. | 50° |
9.下列运算正确的是( )
| A. | 2a3•a4=2a7 | B. | a3+a4=a7 | C. | (2a4)3=8a7 | D. | a3÷a4=a |
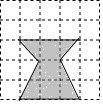 如图,方格图中小正方形的边长为1.将方格图中阴影部分图形剪下来,再把剪下的阴影部分重新剪拼成一个正方形(不重叠无缝隙),那么所拼成的这个正方形的边长为$\sqrt{6}$.
如图,方格图中小正方形的边长为1.将方格图中阴影部分图形剪下来,再把剪下的阴影部分重新剪拼成一个正方形(不重叠无缝隙),那么所拼成的这个正方形的边长为$\sqrt{6}$.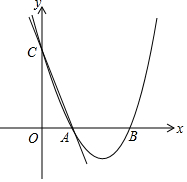 如图所示,直线AC:y=-2x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2 +bx+c(a>0)过A,C两点,与x轴交于另一点B(B在A的右侧),且△OBC∽△OCA.
如图所示,直线AC:y=-2x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2 +bx+c(a>0)过A,C两点,与x轴交于另一点B(B在A的右侧),且△OBC∽△OCA.