��Ŀ����
����Ŀ����ͼ������ƽ��ֱ������ϵ�У����߶�AB���������ֱʱ�����߶�ABΪб����Rt��ABC���ұ�BC��x�ᣬ���AC+BC��ֵΪ�߶�AB��ֱ�Ǿ��룬����L��AB�������߶�AB�������ᴹֱʱ���߶�AB��ֱ�Ǿ��벻���ڣ�
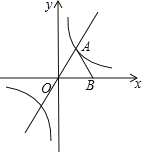
��1����ƽ��ֱ������ϵ�У�A��1��4����B��4��2������L��AB����
��2����ƽ��ֱ������ϵ�У���A������ԭ���غϣ���B��x��y������L��AB����2��
������B��x��y���ڵ�һ����ʱ����֪AC��x��BC��y����AC+BC��L��AB�����ɵ�y��x֮��ĺ�����ϵʽΪ�� ��������x��ȡֵ��Χ���� ������ͼ���л������������ͼ��
����ģ������˼�����̣��ֱ�̽����B�������������Σ���Ȼ��ͼ���зֱ���B�ڶ�������������ʱ��y��x�ĺ���ͼ����Ҫ��д��̽�����̣�
��3����ƽ��ֱ������ϵ�У���A��1��1������������y��a��x��h��2+5�ϴ��ڵ�B��ʹ��2��L��AB����4��
����a����![]() ʱ��ֱ��д��h��ȡֵ��Χ��
ʱ��ֱ��д��h��ȡֵ��Χ��
����h��0���ҡ�ABC�ǵ���ֱ��������ʱ��ֱ��д��a��ȡֵ��Χ��
���𰸡���1��5����2����y����x+2��0��x��2��ͼ�������������y��x+2��y����x��2��y��x��2��ͼ�������������3����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��������
��1�����ݶ���ֱ�Ӽ��㼴�ɣ�
��2������A(0��0)��B(x��y)���ҵ�B(x��y)�ڵ�һ���ޣ�L(AB)��2���ã�x+y��2���Ӷ��õ��𰸣�
�ڸ��ݵ�A��B���꼰��B�������ޣ�L(AB)��2�����������ۼ��ɵó��𰸻���ͼ�Σ�
��3����������������ʱ��Ӧ��h���![]() (x��h)2+5��1����x��h+4��x��h��4���ٷ�������ۣ���������ʽ������⼴�ɣ�
(x��h)2+5��1����x��h+4��x��h��4���ٷ�������ۣ���������ʽ������⼴�ɣ�
����![]() �ǵ���ֱ�������Σ���2��L(AB)��4����������㣬�ֱ���⼴�ɣ�
�ǵ���ֱ�������Σ���2��L(AB)��4����������㣬�ֱ���⼴�ɣ�
�⣺��1����A(1��4)��B(4��2)��
��L(AB)��AC+BC����4��1��+��4��2����5��
��2���١�A(0��0)��B(x��y)���ҵ�B�ڵ�һ���ޣ�L(AB)��2��
��x+y��2��
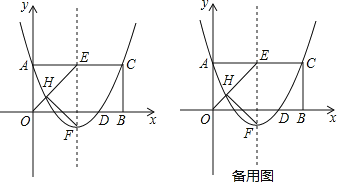
��y����x+2����0��x��2����ͼ����ͼ��ʾ��
�ʴ�Ϊ��y����x+2��0��x��2��
�ڵ�B�ڵڶ�����ʱ����x+y��2��
��y��x+2��ͼ����ͼ��ʾ��
��B�ڵ�������ʱ����x��y��2��
��y����x��2��ͼ����ͼ��ʾ��
��B�ڵ������ޣ�x��y��2��
��y��x��2��ͼ����ͼ��ʾ��
��3���ٵ���![]() (x��h)2+5��1ʱ��x��h+4��x��h��4��
(x��h)2+5��1ʱ��x��h+4��x��h��4��
��![]() ʱ����
ʱ����![]() ��
��![]() ʱ��2��L(AB)��4,
ʱ��2��L(AB)��4,
��![]() ʱ����
ʱ����![]() ��
��![]() ʱ��2��L(AB)��4,
ʱ��2��L(AB)��4,
��h��ȡֵ��ΧΪ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
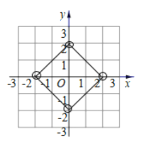
�ڡ�![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��AC=BC��
�֡�L(AB)=AC+BC����2��L(AB)��4��
��1��AB��2��1��BC��2��
����ͼ���������߾���B(2��2)ʱ��L(A��B)��2����ʱ2��4a+5�����a��![]() ��
��
�������߾���B��(3��3)ʱ��L(A��B)��4����ʱ3��9a+5�����a��![]() ��
��
�������߾���B��(��1��3)ʱ��L(A��B)��4����ʱ3��a+5�����a����2��
�۲�ͼ���֪������������a��ֵΪ��![]() ��
��![]() ��
��