题目内容
【题目】阅读下面的材料:
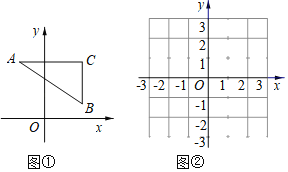
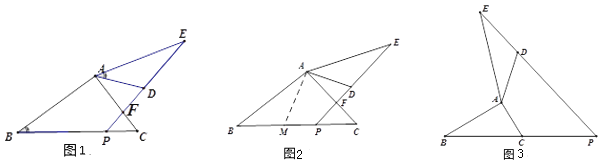
小明同学遇到这样一个问题,如图1,AB=AE,∠ABC=∠EAD,AD=mAC,点P在线段BC上,∠ADE=∠ADP+∠ACB,求![]() 的值.
的值.
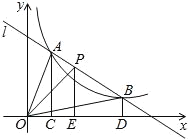
小明研究发现,作∠BAM=∠AED,交BC于点M,通过构造全等三角形,将线段BC转化为用含AD的式子表示出来,从而求得![]() 的值(如图2).
的值(如图2).
(1)小明构造的全等三角形是:_________≌________;
(2)请你将小明的研究过程补充完整,并求出![]() 的值.
的值.
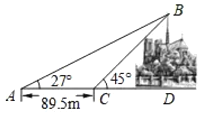
(3)参考小明思考问题的方法,解决问题:
如图3,若将原题中“AB=AE”改为“AB=kAE”,“点P在线段BC上”改为“点P在线段BC的延长线上”,其它条件不变,若∠ACB=2α,求:![]() 的值(结果请用含α,k,m的式子表示).
的值(结果请用含α,k,m的式子表示).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据已知条件直接猜想得出结果;
(2)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,易证
,易证![]() ,再根据
,再根据![]() 结合已知条件得出结果;
结合已知条件得出结果;
(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,得出
,得出![]() ,根据相似三角形的性质及已知条件得出
,根据相似三角形的性质及已知条件得出![]() ,进而求解.
,进而求解.
(1)解:![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
在中![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴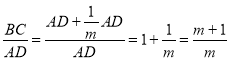 .
.
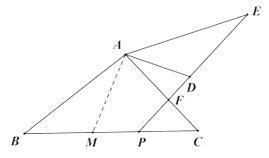
(3)解:过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
在中![]() 和
和![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
过点![]() 作
作![]() .
.
∴![]() ,
,![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
∴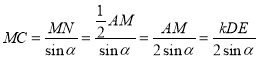 .
.
∴![]()
![]() .
.
∴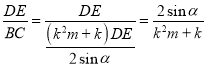 .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目