ĢāÄæÄŚČŻ
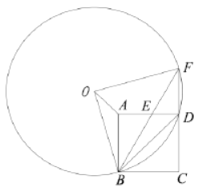
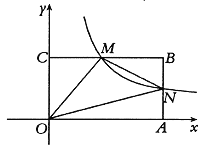
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪAOBC·ÅÖĆŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬±ßOAŌŚyÖįµÄÕż°ėÖįÉĻ£¬±ßOBŌŚxÖįµÄÕż°ėÖįÉĻ£¬Å×ĪļĻߵĶ„µćĪŖF£¬¶Ō³ĘÖį½»ACÓŚµćE£¬ĒŅÅ×ĪļĻß¾¹żµćA£Ø0£¬2£©£¬µćC£¬µćD£Ø3£¬0£©£®”ĻAOBµÄĘ½·ÖĻߏĒOE£¬½»Å×ĪļĻ߶Ō³ĘÖį×ó²ąÓŚµćH£¬Į¬½ÓHF£®
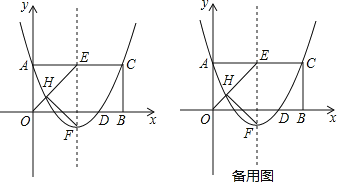
£Ø1£©ĒóøĆÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ŌŚxÖįÉĻÓŠ¶ÆµćM£¬Ļ߶ĪBCÉĻÓŠ¶ÆµćN£¬ĒóĖıߊĪEAMNµÄÖܳ¤µÄ×īŠ”Öµ£»
£Ø3£©øĆÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆĖıߊĪEHFPĪŖĘ½ŠŠĖıߊĪ£æČē¹ū“ęŌŚ£¬Ēó³öµćPµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©y£½![]() x2©
x2©![]() x+2£»£Ø2£©
x+2£»£Ø2£©![]() £»£Ø3£©²»“ęŌŚµćP£¬Ź¹µĆĖıߊĪEHFPĪŖĘ½ŠŠĖıߊĪ£¬ĄķÓɼū½āĪö£®
£»£Ø3£©²»“ęŌŚµćP£¬Ź¹µĆĖıߊĪEHFPĪŖĘ½ŠŠĖıߊĪ£¬ĄķÓɼū½āĪö£®
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅāæÉŅŌµĆµ½CµÄ×ų±ź£¬Č»ŗóøł¾ŻÅ×ĪļĻß¹żµćA”¢C”¢DæÉŅŌĒóµĆøĆÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©øł¾Ż¶Ō³ĘÖįŗĶĶ¼ŠĪæÉŅŌ»³öĻąÓ¦µÄĶ¼ŠĪ£¬Č»ŗóÕŅµ½Ź¹µĆĖıߊĪEAMNµÄÖܳ¤µÄČ”µĆ×īŠ”ÖµŹ±µÄµćMŗĶµćN¼“æÉ£¬Č»ŗóĒó³öÖ±ĻßMNµÄ½āĪöŹ½£¬Č»ŗóÖ±ĻßMNÓėxÖįµÄ½»µć¼“æɽā“š±¾Ģā£»
£Ø3£©øł¾ŻĢāŅā×÷³öŗĻŹŹµÄĶ¼ŠĪ£¬Č»ŗóøł¾ŻĘ½ŠŠĖıߊĪµÄŠŌÖŹæÉÖŖEH£½FP£¬¶ųĶعż¼ĘĖćæ“EHŗĶFPŹĒ·ńĻąµČ£¬¼“æɽā“š±¾Ģā£®
½ā£ŗ£Ø1£©”ßAE”ĪxÖį£¬OEĘ½·Ö”ĻAOB£¬
”ą”ĻAEO£½”ĻEOB£½”ĻAOE£¬
”ąAO£½AE£¬
”ßA£Ø0£¬2£©£¬
”ąE£Ø2£¬2£©£¬
”ąµćC£Ø4£¬2£©£¬
É趞“ĪŗÆŹż½āĪöŹ½ĪŖy£½ax2+bx+2£¬
”ßC£Ø4£¬2£©ŗĶD£Ø3£¬0£©ŌŚøĆŗÆŹżĶ¼ĻóÉĻ£¬
”ą![]() £¬µĆ
£¬µĆ £¬
£¬
”ąøĆÅ×ĪļĻߵĽāĪöŹ½ĪŖy£½![]() x2©
x2©![]() x+2£»
x+2£»
£Ø2£©×÷µćA¹ŲÓŚxÖįµÄ¶Ō³ĘµćA1£¬×÷µćE¹ŲÓŚÖ±ĻßBCµÄ¶Ō³ĘµćE1£¬Į¬½ÓA1E1£¬½»xÖįÓŚµćM£¬½»Ļ߶ĪBCÓŚµćN£®
øł¾Ż¶Ō³ĘÓė×ī¶ĢĀ·¾¶ŌĄķ£¬
“ĖŹ±£¬ĖıߊĪAMNEÖܳ¤×īŠ”£®
Ņ×ÖŖA1£Ø0£¬©2£©£¬E1£Ø6£¬2£©£®
ÉčÖ±ĻßA1E1µÄ½āĪöŹ½ĪŖy£½kx+b£¬
![]() £¬µĆ
£¬µĆ £¬
£¬
”ąÖ±ĻßA1E1µÄ½āĪöŹ½ĪŖ![]() £®
£®
µ±y£½0Ź±£¬x£½3£¬
”ąµćMµÄ×ų±źĪŖ£Ø3£¬0£©£®
”ąÓɹ“¹É¶ØĄķµĆAM£½![]() £¬ME1£½
£¬ME1£½![]() £¬
£¬
”ąĖıߊĪEAMNÖܳ¤µÄ×īŠ”ÖµĪŖAM+MN+NE+AE£½AM+ME1+AE£½![]() £»
£»
£Ø3£©²»“ęŌŚ£®
ĄķÓÉ£ŗ¹żµćF×÷EHµÄĘ½ŠŠĻߣ¬½»Å×ĪļĻßÓŚµćP£®
Ņ×µĆÖ±ĻßOEµÄ½āĪöŹ½ĪŖy£½x£¬
”ßÅ×ĪļĻߵĽāĪöŹ½ĪŖy£½![]() x2©
x2©![]() x+2£½
x+2£½![]() £¬
£¬
”ąÅ×ĪļĻߵĶ„µćFµÄ×ų±źĪŖ£Ø2£¬©![]() £©£¬
£©£¬
ÉčÖ±ĻßFPµÄ½āĪöŹ½ĪŖy£½x+b£¬
½«µćF“śČė£¬µĆ![]() £¬
£¬
”ąÖ±ĻßFPµÄ½āĪöŹ½ĪŖ![]() £®
£®
 £¬
£¬
½āµĆ![]() »ņ
»ņ![]() £¬
£¬
”ąµćPµÄ×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£¬FP£½
£©£¬FP£½![]() ”Į£Ø
”Į£Ø![]() ©2£©£½
©2£©£½![]() £¬
£¬
 £¬
£¬
½āµĆ£¬ »ņ
»ņ £¬
£¬
”ßµćHŹĒÖ±Ļßy£½xÓėÅ×ĪļĻß×ó²ąµÄ½»µć£¬
”ąµćHµÄ×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£¬
£©£¬
”ąOH£½![]() ”Į
”Į![]() £½
£½![]() £¬
£¬
Ņ×µĆ£¬OE£½2![]() £¬
£¬
EH£½OE©OH£½2![]() ©
© ![]() £½
£½![]() £¬
£¬
”ßEH”ŁFP£¬
”ąµćP²»·ūŗĻŅŖĒó£¬
”ą²»“ęŌŚµćP£¬Ź¹µĆĖıߊĪEHFPĪŖĘ½ŠŠĖıߊĪ£®